Hogyan számoljuk ki a kötet egy négyzet piramis

Tér piramis - volumetrikus alakja egy bázissal formájában egy négyzet és háromszög oldalsó élei. A tetején a tér piramis kivetített közepén a bázis. Ha az „a” - oldalán a tér bázis, «H» - piramis magassága (a merőleges csökkent a csúcsa a piramis, hogy a központ a bázis), majd a térfogatot egy négyzet piramis lehet képlettel számítottuk ki: a 2 × (1/3) h. Ez a képlet érvényes bármilyen méretű négyzetes piramis (az ajándéktárgy piramisok egyiptomi piramisok).

lépések szerkesztése

1. módszer a 2:
Térfogatának kiszámításához a terület és magassága szerkesztése

Keresse az oldalán a bázis. Mivel az alapja a tér piramis egy négyzet, az összes bázist egyenlő. Ezért szükséges, hogy megtalálják a oldal hosszát az alap.

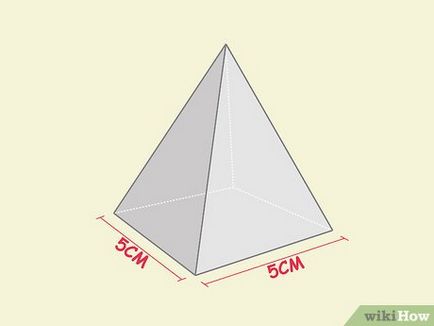
• Például, mivel a piramis bázis oldalán, amely egyenlő 5 cm.
• Ha az oldalán a bázis nem egyenlő egymással, akkor kapnak egy téglalap helyett négyzet piramis. Mindazonáltal, a képlet a térfogata a téglalap alakú piramis hasonló a képlet a kötet egy négyzet piramis. Ha «l» és «w» - két szomszédos (egyenlőtlen) az alsó oldalán a téglalap piramis, a piramis térfogatot alábbi képlettel számítottuk ki: (l × W) × (1/3) H

Számítsuk ki a négyzet alapú terület, megszorozzuk az oldalára önmagában (vagy, más szóval, a felemelő irányban egy négyzet).

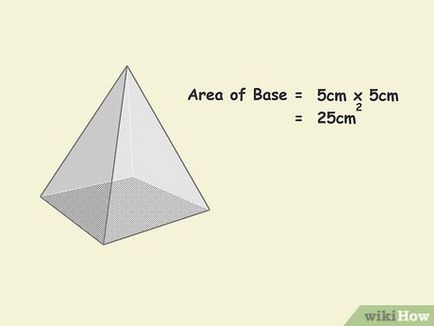
• A mi példánkban, 5 x = 5 5 2 = 25 cm 2.
• Ne felejtsük el, hogy a terület mért tér egységek - négyzetcentiméter, négyzetméter, négyzetkilométer, és így tovább.

Szorozzuk meg a területet, a bázis a magassága a piramis. Magasság - a merőleges csökkent a csúcsa a piramis alapja. Megszorozzuk ezeket az értékeket, akkor kap egy térfogatú kocka az azonos alapja és magassága, mint a piramis.

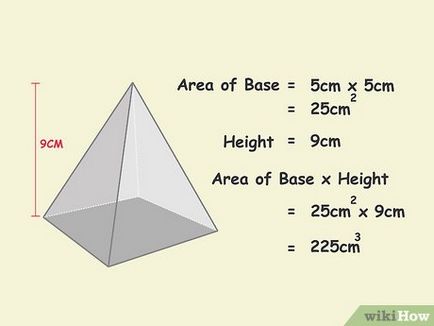
• Ebben a példában, a magassága 9 cm 25 cm 2 cm × 9 cm 3 = 225
• Ne felejtsük el, hogy a térfogatot köbméterben egységek, ebben az esetben, a köbcentiméter.

Osszuk meg az eredményt 3 és megtalálod a kötet egy négyzet piramis.

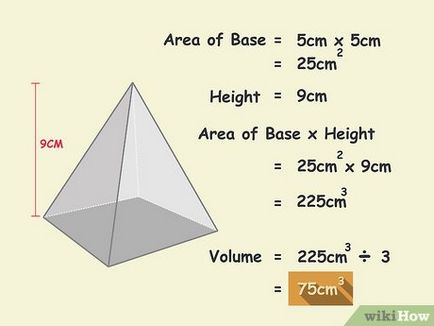
• Ebben a példában, 225 cm 3/3 = 75 cm 3.
• Volume mérjük köbös egység.

2. módszer 2:
Kiszámítása mennyiségének apothem szerkesztése

Ha van megadva vagy terület vagy magassága a piramis és apothem, megtalálja a kötet egy piramis, a Pitagorasz-tétel. Apothem - a magassága a lejtő háromszög arcok a piramis, levonni a csúcsai a háromszög alapja. Kiszámításához apothem használja az oldalsó a piramis alapja és magassága.

• Apothem osztja az oldalán az alap felét, és vágja derékszögben.

Vegyünk egy derékszögű háromszög alakult apothem magassága és a szegmens összekötő közepén a bázis és a közepén a kezét. Ez háromszög átfogója apothem, amely megtalálható a Pitagorasz-tétel. Szegmens összekötő a központ a bázis és középső részén, felével egyenlő a bázis oldalán (ebben a szegmensben az egyik lábát, a láb a második magassága a piramis).

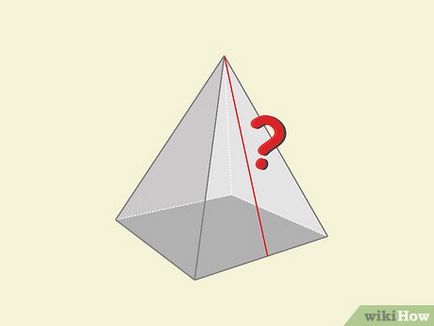
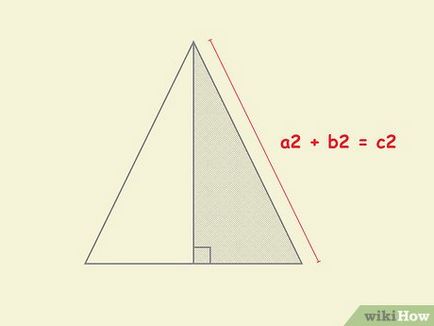
• Emlékezzünk vissza, hogy Pitagorasz-tétel felírható: a 2 + b 2 = c 2, ahol «a» és «b» - a lábak, a «C» - az átfogó egy derékszögű háromszög.
• Például adott egy piramis, amelynek alapja oldala 4 cm, és apothem - 6 cm érdekében, hogy megtalálják a magassága a piramis, helyettesíteni ezeket az értékeket a Pitagorasz-tétel ..
  • a 2 + b 2 = c 2
  • egy 2 + (4/2) 2 = 6 2
  • 2 = 32
  • a = √32 = 5,66 cm talál a második szakasza a derékszögű háromszög, amelynek a magassága a piramis (hasonlóképpen, ha kapnának apothem és a magassága a piramis, meg tudná találni a fele az alapja a piramis).

Használja talált érték, hogy megtalálják a mennyiség a piramis a következő képlettel: 2 × (1/3) h.

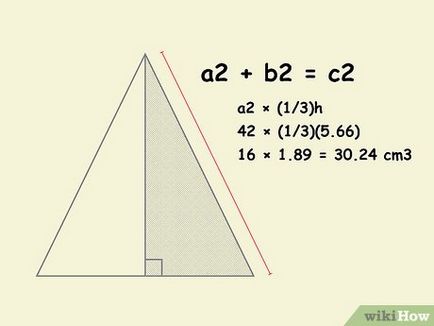
• A példánkban már kiszámította, hogy a magassága a piramis 5,66 cm helyettesítő értékek a képletet a térfogata a gúla .:
  • 2 × (1/3) H
  • Április 2 × (1/3) (5,66)
  • 16 × 1,89 = 30,24 cm3.

Ha az előírtnál apothem használja a szélén a piramis. Rib - egy szegmens, amely összeköti a tetején a piramis a tetején a tér alján a piramis. Ebben az esetben kapsz egy derékszögű háromszög, a lábak, amelyek magassága a piramis és a felét a négyzet átlója az alapja a piramis, és az átfogó - a szélén a piramis. Mivel a négyzet átlójának egyenlő √2 × oldalán a tér, megtalálja a oldalán a tér (ek) elosztjuk az átlós √2. Akkor lesz képes megtalálni a kötet egy piramis fenti képlet.

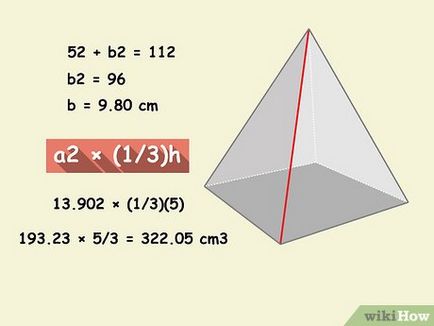
• Például, adott egy négyzet gúla magassága 5 cm és 11 cm széle Számítsuk fele átlós következőképpen .:
  • Május 2 + b 2 = 11 2
  • b 2 = 96
  • b = 9,80 cm.
  • Azt találtuk fele átlósan, így a diagonális egyenlő: 9,80 cm × 2 = 19,60 cm.
  • egy négyzet oldala (bázis) egyenlő √2 × diagonális, így 19,60 / √2 = 13,90 cm Most megtalálják a térfogata a gúla által képletű :. 2 × (1/3) H
  • 13.90 2 × (1/3) (5)
  • 193,23 × 5/3 = 322,05 cm 3