Hogyan lehet hajtani a papírt, és kap ez a Holdra

Ismerete elveinek mértani segít a mindennapi életben, az eredményszemléletű kamat a betét, a tanulás terjedésének sebességét járványok. Továbbá, a mértani középpontjában a híres paradoxon, kihívást tudásunkat végtelenig.

Vegyünk egy újságpapírt. Hányszor tudsz hajtsa félbe? A valós világban, legfeljebb hétszer (próbálni). De tegyük fel, hogy tudjuk, hogy ezt a lapot, ahányszor csak akarjuk. Tehát, ha tesz egy papírt mindössze 45-szer, a rétegek vastagsága lesz olyan magas, hogy kapnánk, hogy a hold.

Lássuk, miért.

Tegyük fel, hogy egy újság lemezvastagság 0,001 cm Ha hajtogatott lap felét, vastagsága megduplázódott, és lesz 0,002 cm és minden egymás utáni hozzáadásával vastagságának a fele fog menyatsyav összhangban szekvenciával: .. 0,001 cm, 0,002 cm, 0,004 cm, 0,008 cm, 0,016 cm 0,032 cm ...

Összecsukható a lapot félbe tízszer. kapunk egy újságot vastagsága 1 cm x 10 -3 * 2 10 vagy 1024, lásd, hogy egy kicsit több, mint egy centiméter. Meg kell megállapítani 17-szer - nem probléma - kap egy 1 cm x 10 -3 17 * 2 = 131 cm, magassága az átlagos hobbit.

A viccek felett, most komolyan.

Fold harmincszor - csaknem tíz kilométeres (1 cm x 10 -3 * 2 30). Ebben a magasságban a repülőgépek repülni! Negyven alkalommal - majdnem 11 000 km-re (1 cm x 10 -3 40 2 *). Houston van egy rés! Ebben a magasságban pályára műholdat állított pályára: 43 alkalommal: 87 961 km, 44 alkalommal: 175921 km, 45 alkalommal: 351 844 km. Stop! Elértük a hold! Ha felvesz egy papírt még egyszer, aztán mehetünk vissza a Földre!

Ez a típus az úgynevezett exponenciális növekedés (exponens - kitevő). Az ő „robbanásveszélyes” természet szembe a „lassú” vonal és a teljesítmény növelésére.

A sorszámok kapott példája egy újság, egy mértani sorozat.

Mértani - számszerű sorrendben b 1. b2. b3. ahol minden egyes egymást követő kezdődő szám a második van kialakítva az előző megszorozva egy bizonyos számú q (nevező progresszió). Ebben az esetben, b1 ≠ 0 és q ≠ 0, egyébként csak kap nullák szekvenciát.

ahol n - egész szám.

Felhívjuk figyelmét, hogy mindent tudni exponenciálisan kell, de csak három paraméter: az érték az első elem b1. a progresszió q, és a tagok száma n. A példában a kezdeti vastagsága a papírlap szolgált az első elem, és az a tény, hogy hozzáadásával a lemez újság a vastagság feléig megduplázódik, ami nekünk a értéke q = 2. Tekintettel arra, hogy minden progresszió elem képviseli, mint egy milliárd = b1 * q ( n-1):

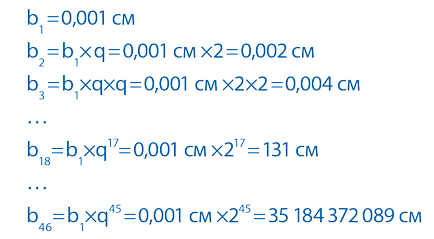
Csakúgy, mint a számtani sorozat, néha ki kell számítani az összeg minden eleme progresszióját. Csináljunk egy kis trükk. Írunk az egyenlet a következőképpen, majd vonjuk ki a második egyenletből az első:

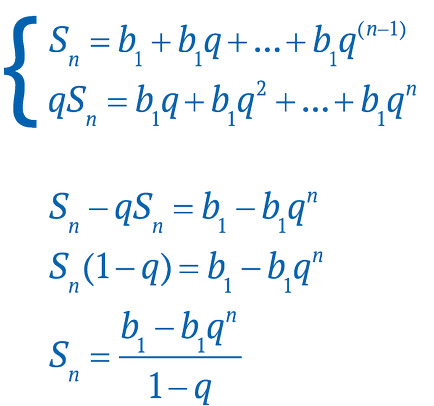
Így megkapjuk a képlet az összeg véges számú geometriai elemek.

Mértani az alapja a híres paradoxon, kihívást tudásunkat végtelenig.

És mi van, ha az elemeket a progresszió végtelen számú? Tudunk majd kiszámítja az összeget e progresszió? Viselkedés exponenciálisan, és ez határozza meg az összeg a progresszió q. És szinte minden q értéke semmi szokatlan történik, az összeget a végtelen számú geometriai elemek nem vezet valami véges. Azaz, a szórás, ha a matematika nyelvén.

Azonban, az esetben, ha a mértani végtelen számú elemek és a nevező kisebb, mint az egység (q<1 ) представляет особый интерес.

Az intuíció azt mondja, hogy az összeg a végtelen számú pozitív elemet kell, nos, legalábbis végtelen. Igaz ez? Ebben a kérdésben tükrözte drevnegrecheskiyfilosof Zenon Eleysky, hogy a jövőben, ezek a gondolatok lett az alapja az úgynevezett paradox kettősség paradoxon vagy szétválasztási kettő.

Miután egy eredményes nap gondolkodási, Zeno úgy döntött, hogy sétálni a parkban található, az otthona közelében. Tegyük fel, hogy a távolság a park egy kilométerre, és Zeno egy sebesség 1 km / h. Meddig tart egy séta?

Íme az érvek Zeno. Ahhoz, hogy elérjük a parkban, akkor először meg kell menni félúton - ½ kilométeres, igaz? Tart ½ óra. Amint odaért a közepén az út, akkor kell átmenni a fele a hátralévő távolságot - ¼ kilométer. És ez viszont fog ¼ óra. Továbbá, ez fog történni ebben az időben, és újra. És továbbra is így örökké.

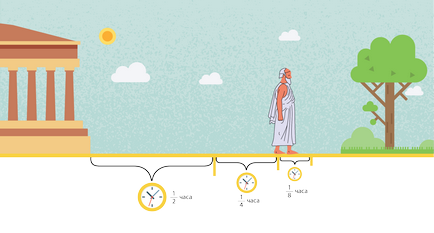
Szóval, milyen hosszú Zeno menne a parkban? Ahhoz, hogy erre a kérdésre válaszolni, meg kell adni az összes időszakok, amelyek költöttek minden részének útját. A probléma azonban az, hogy egy ilyen végtelen számú alkatrész!

Felhívjuk figyelmét, hogy a következő ciklusban a szekvencia növeli a:

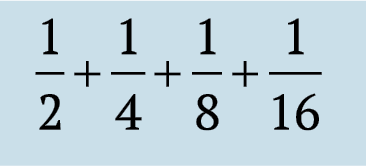
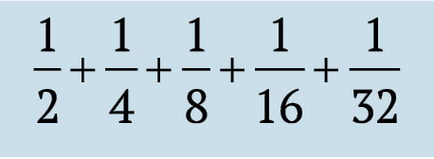
ami viszont kevesebb, mint

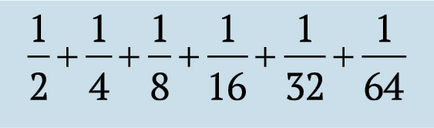
és így tovább. Ez a mi összeg az egymást követő elem nőtt, és a tagok száma egyre végtelenül nagy, mint a mi esetünkben, az összeg tovább fog növekedni a végtelenségig. Következésképpen egy séta a parkban tart végtelen mennyiségű idő, más szóval, hogy soha nem lesz a parkban!

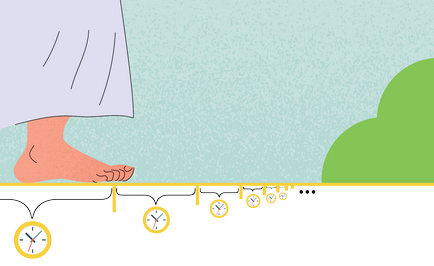
Ez a paradoxon. Egyrészt, van dolgunk egyértelműen indokolt a Zeno, aki azt állítja, hogy minden mozgás lehetetlen, de a többi - tudjuk álljon fel és járj a hűtőszekrénybe. Az első gondolat, ami akkor fordul elő - abszurd!

De Zeno érvelése elme elfoglalt matematikusok és filozófusok évezredek óta, hogy elmélyült megértése végtelenbe és folytonosság.

Hol a hiba a logika Zeno? Ennek része egy matematikai modellt a mozgás a séta egyszerű. Valóban, az utazási idő - a távolság osztva a sebességet, ezért a becsült időt sétál - egy órát.

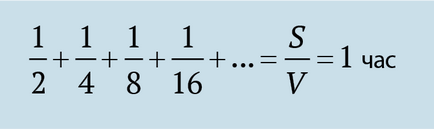
Mint később kiderült, a matematika, vannak esetek, amikor ez lehetséges összefoglalni végtelen számú elemet, és kap a végső választ. Azaz, ahogy a matematikusok mondják, a sorozat konvergál. A mi esetünkben, végtelen mennyiségű időrések egyenlő (konvergál) egy óra.

Mint láttuk, a végtelen kapott szekvencia Zeno, egy mértani. És az összeg ennek progresszió konvergens. Figyeljük meg a közös nevező a progresszió? Ez egyenlő ½. Kiderült, hogy ha q> -1 q<1 сумма бесконечной геометрической прогрессии сходится. Давайте вспомним формулу для конечной прогрессии и переделаем ее для бесконечного случая.

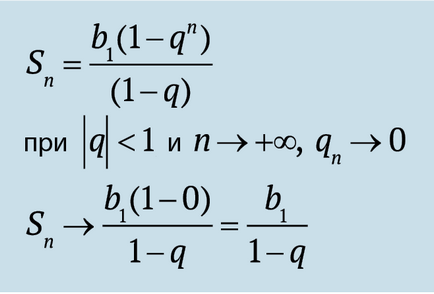
Összefoglalva, szeretném még egyszer felhívni a figyelmet arra a tényre, mint a választás a progresszió q határozza meg a viselkedést egy mértani. Exponenciális növekedés exponenciális bomlás. Utazástól, hogy a hold egy darab papírt, és az ilyen kis értékű, hogy az összegük, akár végtelen, nem számít.