Empirikus eloszlásfüggvény

Let nx - a megfigyelések száma, amelyekben az érték a jel-X x-nél kisebb. Amikor egy minta mérete egyenlő n-nel, a relatív gyakorisága az esemény-értékű X <х равна nx /n .

8. meghatározása Function

meghatározzuk minden egyes értékére a relatív gyakorisága az esemény X X <х, называется эмпирической функцией распреде-ления, или функцией распределения выборки.

Ezzel szemben a empirikus eloszlásfüggvény F * (x) mintaelosztó függvény F (x) általános sovokupnos perces nevezzük az elméleti eloszlásfüggvényt. Time-különbség a kettő között az, hogy az F (x) meghatározása után szeretné beállítani a valószínűsége esemény X <х, a F*(x) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших п вероятность отличия этих функций друг от друга близка к единице:

Könnyen belátható, hogy az F * (x) az összes tulajdonságait F (x), ami meghatározásából következik (18,49):

1) értékeket az F * (x) tartozik a [0, 1];

2) F * (x) csökkenő függvénye;

Az ugyanazon függvény F * (x) értékelésére használják az elméleti eloszlásfüggvény F (x) a teljes népesség.

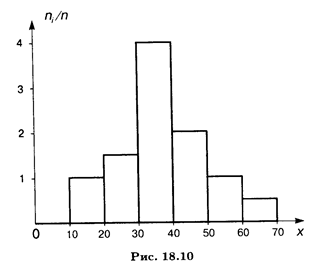
3. példa Construct empirikus eloszlásfüggvény egy adott minta:

Határozat. A minta mérete n = 10 + 15 + 25 = 50. A legalacsonyabb kiviteli alak megegyezik a 2, így az F * (x) = 0 x ≤ 2. Az X értéke <4 (или x1 = 2) наблюдалось 10 раз, значит, F*(x) = 10/50 = 0,2 при 2 <х <4. Значения X <6 (а именно x1 = 2 и x2 = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 <х <6 функция F*(x) = 25/50 = 0,5. Поскольку x = 6 — максимальная варианта, то F*(x) = 1 при х> 6. Írja képlet a szükséges tapasztalati funkció:

A grafikon az ezt a funkciót a ábrán látható. 18.8.

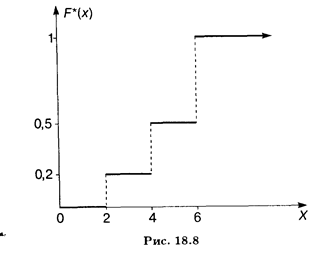
Polygon és hisztogram

Minden pár értékek (XI. Ni) eloszlási minta lehet értelmezni, mint egy pont a koordináta síkon. Pontosabban, de azt is lehet venni egy pár értékek (x i. Wi) Ments vonatkozó eloszlása ​​a mintában. Sokszög vonalszakaszok összekötő pontok (XI. Ni), az úgynevezett poligon frekvenciák. Lo manaya kapcsolódási pont a koordinátarendszerben (XI. Wi), az úgynevezett poligon relatív gyakoriságokat. Ábra. 18.9 mutatja a sokszög relatív gyakorisági eloszlását a 2. példában adjuk.

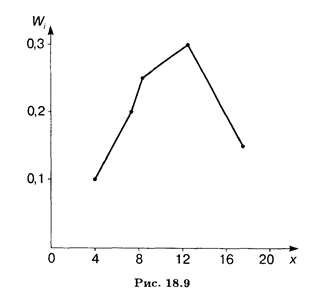
Arra az esetre folytonos jellemző X kényelmes osztani in-intervallum (xmin. Xmax) annak megfigyelt értékek több részintervallumok hosszúságú h minden, és segítenek megtalálni a felsorolt ​​intervallumok összeg nj frekvenciákat. megütötte. Szakaszai chataya-alakú álló téglalapok bázis hosszúságúak, és magassága h nj / h (frekvencia sűrűség) nevezzük a hisztogram frekvenciákat. A geometriai jelentését a hisztogram: ez könnyen belátható, hogy a területe egyenlő az összessége a frekvencia vagy a minta térfogata. Ábra. 18.10 ábra egy hisztogram Ob-EMA n = 100.

Hasonlóképpen határoztuk meg, és egy hisztogram a relatív frekvenciák esetén-ing magassága téglalapok alkotó lépcsős alakja sheniyami otno meghatározott mennyiségű relatív frekvenciatartományban (xmin + (j - 1) h xmin + JH.), A hossza intervallum H, vagyis E-érték Wj / h. Könnyen belátható, hogy a terület a hisztogram a relatív frekvencia megegyezik az egység (összege a relatív mintavételi frekvencia).