Empirikus eloszlásfüggvény - studopediya

Meghatározása 25.2.Empiricheskoy eloszlásfüggvény (mintavételi funkció) hívás funkciót, meghatározzuk minden egyes értékére a relatív gyakorisága az esemény, azaz

ahol - számos kisebb; - a minta nagysága.

Tól Bernoulli-tétel az következik, hogy egy kellően nagy a minta mérete és jellemzői alig különböznek egymástól. Ellentétben az empirikus eloszlásfüggvény az elméleti van az, hogy az elméleti eloszlás határozza meg a valószínűsége az esemény, és az empirikus funkció határozza meg a relatív gyakoriságát ugyanazon esemény.

Empirikus eloszlásfüggvény rendelkezik minden ingatlan eloszlásfüggvény:

1) értékeket az empirikus eloszlásfüggvény tartoznak a szegmens;

2) - egy nem-csökkenő függvény;

3) amennyiben - a legkisebb kiviteli alakban, amikor; ha - a legnagyobb változat, mikor.

Példa 25.1. A konstrukció egy empirikus eloszlásfüggvényt ebben a mintában:

Határozat. Találunk minta mérete: 18 + 12 + 30 = 60.

2. A legalacsonyabb kiviteli alak ezért a.

Érték, nevezetesen volt 12-szer, ezért a.

Érték, nevezetesen, és a megfigyelt 12 + 18 = 30-szor, tehát, ha.

Mivel - a legnagyobb változat, mikor.

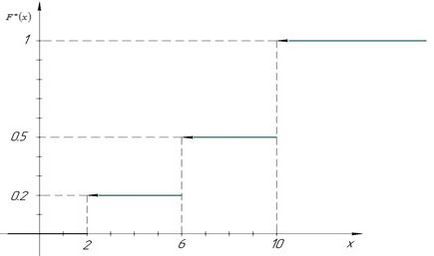
Keresek empirikus függvény

A grafikon az ezt a funkciót a következő: