Alapvető trigonometrikus azonosságok, a kimenet a képletek

Ebben a cikkben, akkor teljes mértékben figyelembe az alapvető trigonometrikus azonosságok. Alapvető trigonometrikus azonosságok egyenlő megteremti a kapcsolatot a szinusz, koszinusz, tangens és a kotangensét a szög, és lehetővé teszi, hogy megtalálja ismert bármilyen trigonometrikus függvények egy másik.

Azonnal felsorolni az alapvető trigonometrikus azonosságok, amelyek elemzik ebben a cikkben. Írja be őket a következő táblázat ad levezetése ezeket a képleteket, és adja meg a szükséges magyarázatot.

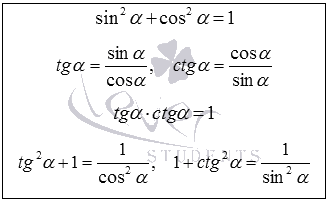
Oldalnavigáció.

A kapcsolat a szinusz és koszinusz az a szög

Ez különösen érdekes az egyenlőséget, amely adta a nevét az alap trigonometrikus azonosságok.

Mielőtt igazoló pitagoreus trigonometrikus identitását, így annak megfogalmazása: a négyzetének összege a szinusz és koszinusz az a szög azonos egyenlő eggyel. Most bizonyítani.

Utalva az egység kör. Tegyük fel, hogy a kezdőpont A (1, 0) bekapcsolása után keresztül szögben az A1 pontját. A meghatározások a szinusz és koszinusz az A1 pont koordinátái. Továbbá, A1 fekszik a készülék kör, ezért a koordinátákat kell felelniük az egység kör, amely az x 2 + y 2 = 1. Vagyis, nem kell az egyenlőséget. Ez azt bizonyítja, a Pitagorasz trigonometrikus azonosság minden elfordulási szögek.

Egyenlőség gyakran nevezik a Pitagorasz-tétel trigonometria. Hadd illusztráljam ezt a pontot.

Vigye a készüléket kört. Forgatás a kezdőpont A (1, 0) pont körüli O szögben. Legyen az A pont után a forgási válik A1 pont (x, y). Csökkenés a pont A1 A1 H egyenesre merőleges Ox.

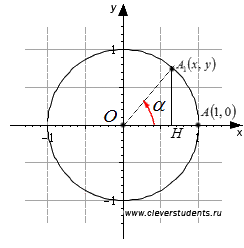
Tekintsük téglalap alakú háromszög OA1 H. világosan látható, a találmány, hogy a hossza a lábak A1 H és OH rendre az abszcissza és ordináta A1 modul pontot. azaz, | A1 H | = | y | és | OH | = | x |. OA1 és a hossza a átfogója egyenlő a sugara egységnyi kör, azaz | OA1 | = 1. Pitagorasz-tétel lehetővé teszi számunkra, hogy írjon az egyenlőség | A1 H | 2 + | OH | 2 = | OA1 | 2. mi lehet átírni | y | 2 + | x | 2 = 1 vagy 2 y 2 + x 2 = 1. De, definíció szerint, majd a következő egyenlet y 2 + x 2 = 1, akkor elmozdulni egyenlőséget.

Pitagorasz-trigonometrikus azonosság esetén gyakran használatos konvertáló trigonometrikus kifejezések. Ez lehetővé teszi a négyzetének összege a szinusz és koszinusz az a szög a készülék cserélni. Legalább egy része az alapvető trigonometrikus azonosságát használjuk fordított sorrendben: az egység helyére a négyzetének összege a szinusz és koszinusz egy szög.

Érintő és kotangensét a szinusz és koszinusz

Identitások összekötő érintő és kotangensét a szinusz és koszinusz a szög az egyik fajta, és azonnal követi a meghatározások szinusz, koszinusz, tangens és kotangens. Valóban, definíció szerint, van egy szinusz ordináta y, a koszinusz metszék X, az érintő az aránya az ordináta a metszék, azaz, egy rácsos az aránya az abszcissza a ordináta, azaz.

Ennek köszönhetően nyilvánvaló identitás és gyakran meghatározza az érintő kotangensét adott nem arányát az abszcissza és az ordináta, és az arány a szinusz és koszinusz. Tehát a tangense szöget az aránya a szinusz a cosinus a szög, és kotangensét - az arány a szinusz a koszinusz.

A rész lezárásához meg kell jegyezni, hogy az identitás és van egy hely, minden a szögek, amelyek tagjai ezeket a trigonometrikus függvények értelmezhető. Tehát a képlet érvényes minden más, mint a (különben a nevező nulla és a nullával való osztást, mi nem határozza meg), és a képlet - minden más, mint ahol a z - bármilyen egész szám.

A kapcsolat a tangens és kotangens

Még nyilvánvalóbb trigonometrikus azonosságok, mint az előző kettő, az identitás összekapcsolása az érintő kotangensét a látószöget. Egyértelmű, hogy ez igaz bármilyen szögben eltérő, egyébként sem az érintő vagy kotangensét nincs definiálva.

Igazolása a képlet nagyon egyszerű. A meghatározás szerint, valamint adott. Ez lehet elvégezni a bizonyítást és egy kicsit más. Tehát tetszik, akkor.

Tehát érintő és kotangensét a szög, ahol van értelme, van egy kölcsönös számát.

A tangens és koszinusz, szinusz és kotangens

Végül elérkeztünk az utolsó két alapvető trigonometrikus azonosságok. Ők csatlakozni az érintő és a sinus és cosinus és kotangensét a szöget.

Itt van a készítmény: az összege a tér a szög tangense és az egységek számát egyenlő az inverze a tér a koszinusza a szög, és az összeg a tér az egység és a kotangensét a szög egyenlő a reciproka a tér a szinusz a szög.

Következtetés Ezek a képletek végezhetjük, kezdve az alapvető trigonometrikus azonosságok faj. Ha elosztjuk mindkét oldalán az egyenlet által (ebben az esetben természetesen nem egyezhet nulla), megkapjuk a képlet. Ha mindkét fél osztva (ez nem egyezhet nulla), eljutunk a személyazonosságát.

Így az azonosság minden elkülönülő, és identitás - bármely más, mint.