A távolság a kitérő egyenes
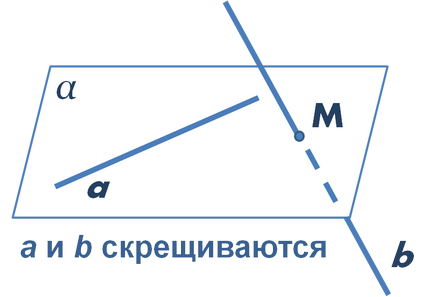
Ebben a cikkben egy példát a probléma megoldásának a C2 USE szétszerelt módszert kell találni a távolságot a kitérő egyenes keresztül koordináta módszerrel. Emlékezzünk vissza, hogy a vonalak skreschivayuschi-Misia, ha nem egy síkban fekszik. Különösen, ha az egyik sorban egy síkban fekszik, és a második egyenes metszi ezt a síkot egy olyan ponton, amely fekszik az első egyenes, ezek egyenes vonalak ferde (lásd. Ábra).
Ahhoz, hogy megtalálja a távolságot a ferde vonalak köteles:
- Keresztül a közvetlen egyik ferde sík, amely párhuzamos a másik ferde vonalak.
- Alsó merőleges bármely pont a második egyenes kapott síkban. A hossza a merőlegesek lesznek a kívánt távolságot a sorok között.
Nézzük meg az algoritmus részletesen a példa a probléma megoldásának a C2 vizsga matematikából.
A távolság a két egyenes között a térben
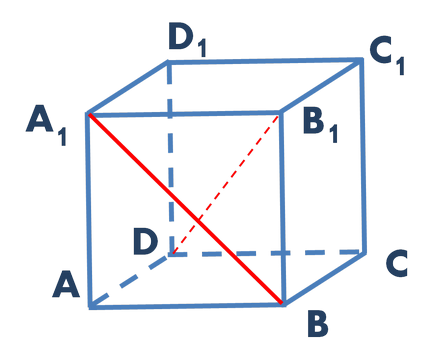
Ábra. 1. tervek feladat
Határozat. DB1 átlósan közepén keresztül a kocka (O pont) rajzolásához párhuzamos egyenes vonal A1B. A metszéspontok az egyenes BC és A1D1 bordák rendre jelöljük N és M. Közvetlen MN MNB1 egy síkban fekszik párhuzamos vonal és A1B. amely ebben a síkban nem hazudik. Ez azt jelenti, hogy a vonal párhuzamos A1B MNB1 sík alapján a párhuzamos vonal és egy sík (ábra. 2).
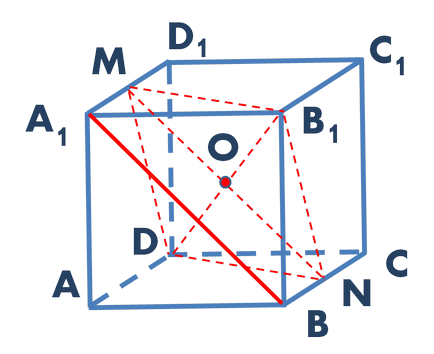
Ábra. 2. A szükséges távolságot a ferde vonalak egyenlő távolságra legyen minden pontján a kiválasztott vonal képsíkjához
Keresünk most a távolság bármely pontján a sort a A1B MNB1 gépet. Ez a távolság lesz, definíció szerint, a kívánt távolságot a ferde vonalak.
Annak meghatározására, ez a távolság használatával a koordinátákat. Bemutatunk egy Descartes-féle derékszögű koordináta-rendszert úgy, hogy kezdőpontja egybeesik a B pont, X tengely mentén irányul élek BA. széle mentén BC - Y tengely. Z tengely - a széle mentén BB1 (3. ábra).
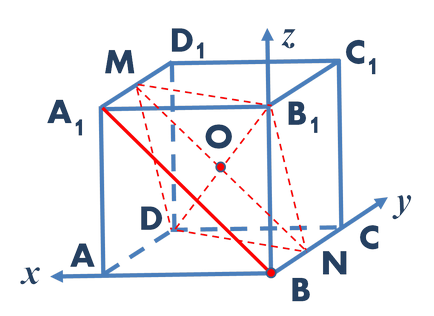
Ábra. 3. A Descartes-féle derékszögű koordináta-rendszer úgy van megválasztva, hogy amint az ábrán
MNB1 megtalálják az egyenlet a sík koordináta-rendszer. Ehhez a pontok koordinátáinak meghatározásához először M. N és B1. A kapott koordináták helyettesítő az általános egyenlete egy egyenes vonal, és így a következő egyenletrendszert:
A második egyenletből kapjuk a harmadik megkapjuk majd egy első szerezni behelyettesítve a kapott értékeket az általános vonal egyenlete:
Azt észleltük, hogy egyébként MNB1 sík átmegy az origón. Azt ossza mindkét oldalán az egyenlet és kap:
A távolság egy pont egy meghatározott síkra, amelyet a képlet:
ahol - a pont koordinátáit B. - együtthatók a változók a sík egyenletét. B pont koordinátái végül megszerezni: