3) Kis mennyiségű és kofaktorok

razlozheniya.Minormatritsy képletekben A - a meghatározója négyzetes mátrixa érdekében k (amely más néven a sorrendben a kisebb), amely a mátrix elemei egy a kereszteződésekben a sor számok és oszlop számokat.

Ha a számok egyeznek sorokat számokkal jelölve jelölt oszlopokban, az úgynevezett minor fő. és ha volt az első k sora és az első k oszlopok - szögletes vagy vezető főnök.

Adott esetben kisebb elem mátrix n-edik rendű az a meghatározó a sorrendben (n-1), amely megfelel a mátrix, amely nyert a mátrix törlésével az i-edik sorának és j-edik oszlop.

Alap kisebb a mátrix bármely nem nulla kisebb maximális sorrendben. Kisebb volt az alap, szükséges és elégséges, hogy minden annak határos kiskorúak (azaz, amely a kiskorúak egyike által magasabb fokú) nulla lenne. A rendszer vonalak (oszlopok) a mátrix társított bázis kisebb, egy maximális lineárisan független alrendszer az összes sort (oszlopok) mátrix.

Például egy mátrix:

Tegyük fel, hogy meg akarja találni egy további kisebb. Ez a kisebb - a meghatározója a mátrix, amelyet úgy kapunk, törli a sort, a 2. és 3. oszlop:

Kofaktor az elemszám matritsynazyvaetsya

,

ahol - további Minor. meghatározója a mátrix nyert a mátrix eredeti és törlési által az i-edik sorának és j-edik oszlop.

A név „a kofaktor” kapcsolódik a képletek bomlás a meghatározó egy mátrix sor (oszlop):

Lemma a bővítés meghatározó hamis állítások, hogy

Ezeket az állításokat kell algoritmust találni az inverz mátrix:

cserélni minden eleme az eredeti mátrix kofaktor,

A kapott mátrix transzponáltja - Adjungált kapunk eredményeképpen,

osztani minden eleme a mátrix az Unió a meghatározó az eredeti mátrix.

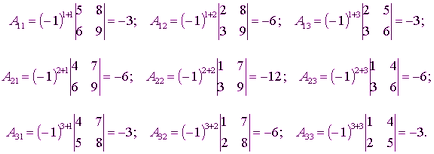
döntő

Bemutatjuk a meghatározása a meghatározója négyzetes mátrix tetszőleges sorrendben. Ez a meghatározás rekurzív. azaz, hogy meghatározzák, mi az a meghatározó a mátrix a rend, meg kell tudni, hogy mi az a meghatározó a mátrix a rend. Azt is vegye figyelembe, hogy egyetlen meghatározó négyzetes mátrixok.

A meghatározója négyzetes mátrix fogja jelölni vagy det.

Meghatározása 1.Opredelitelem négyzetes mátrix az úgynevezett másodrendű számát.

Meghatározója négyzetes mátrixa érdekében, hívott szám

ahol - a sorrendben a meghatározója a mátrix nyert a mátrix törlésével az első sor és oszlop száma.

Az érthetőség kedvéért írunk, hogyan kell kiszámítani a meghatározója a negyedrendű mátrix:

Megjegyzés. A tényleges számítás meghatározói mátrixok magasabb, mint a harmadik rend meghatározása alapján a kivételes esetekben alkalmazható. Általános szabály, hogy a számítást végezni más algoritmusokat, amelyek később tárgyaljuk, és amely kevesebb számítástechnikai tevékenység.

Megjegyzés. Meghatározásában 1 pontosabb lenne azt mondani, hogy a determináns egy függvény a készlet négyzet mátrixok rend és értékek egy számsor.

Megjegyzés. A szakirodalomban, ahelyett, hogy a „determináns” is használják a „determináns”, amelynek ugyanaz a jelentése. A szó „meghatározó”, és volt egy jelölést det.

Vegyünk néhány tulajdonságait meghatározó, amelynek van kiszerelve, mint nyilatkozatok.

Állítás 1. Ha átültetés a meghatározó nem változik, ez van.

2. igénypont szerinti meghatározó terméket négyzetes mátrixok a termék a tényezők meghatározó, azaz.

Állítás 3. Ha a mátrix-swap két sor, akkor annak meghatározó előjelet.

Nyilatkozat 4. Ha a mátrix két azonos sorban, determinánsa nulla.

A jövőben, akkor meg kell adni egy sort, és szorozzuk száma húr. Ezek az intézkedések a sorok (oszlopok), akkor jól teljesíteni, mint az intézkedések egy sor mátrix (oszlop mátrix), azaz az egyes elemek. Az eredmény fog szolgálni sor (oszlop), mint általában, nem esik egybe vonalak az eredeti mátrix. Ha vannak sorok a kiegészítések (oszlop) és megszorozzuk azokat száma beszélhetünk lineáris kombinációja a sorok (oszlopok), azaz az összeg numerikus együtthatók.

Állítás 5. Ha egy sor a mátrix szorozni egy számot, majd a determináns szorozni ezt a számot.

Nyilatkozat 6. Ha a mátrix egy üres karakterlánc, akkor determinánsa nulla.

Elfogadása 7. Ha az egyik a többi sor a mátrix számának szorzatával (arányos a vonal), majd a meghatározója a mátrix egyenlő nullával.

Elfogadása 8. Hagyja a mátrix i-edik sorának a formája. Ezután, amennyiben az előállított mátrix a mátrix helyett i-edik sorról sorra, és a mátrix - helyett i-edik sorról sorra.

Állítás 9. Ha az egyik sort a mátrix, hogy újabb, szorozva a szám, meghatározója a mátrix nem változik.

Tétel 10. Ha az egyik sort a mátrix egy lineáris kombinációja a másik sor, hogy a determináns a mátrix egyenlő nullával.

Meghatározása 2.Algebraicheskim mellett az elem a mátrix egy szám egyenlő, ahol - a meghatározója a mátrix nyert a mátrix törlésével az i-edik sorának és j-edik oszlop. Algebrai Amellett, hogy a mátrixelem jelzi.

Példa. Let. majd

Megjegyzés. A ko-faktorok, 1. meghatározás meghatározó felírható:

4) és annak fordított mátrixba számítás. A fordított mátrix - mátrix szorzás eredménye, amelyen az eredeti mátrixot az identitás mátrix.

Kiszámítani a fordított mátrix, adja meg az értéket a sorok számát a matricát és az oszlopok száma, majd adja meg az értékeket a mátrix elemeinek, majd nyomja meg a „Számítás” gombot. Az eredmény a program lesz az inverz mátrix. Az eredeti mátrix és a számított inverz mátrix lehet másolni a vágólapra más alkalmazások.