WolframAlpha orosz

Sőt, ha tudjuk, hogyan kell helyesen használni WolframAlpha, akkor nem valószínű, hogy kell folyamodni a hatalmat sorozat közelítő számítások: a mechanizmus a közelítő számítások épített Wolfram Alpha alapértelmezés (mint, sőt, bármilyen zsebben számológép). Azonban WolframAlpha rendszer nagyon hasznos, amikor szükség van, hogy könnyedén illusztrálják, hogyan teljesülnek közelítő számítások segítségével hatványsor.

Korábban úgy vélték, hogyan lehet bővíteni a funkciót egy hatványsor. A bővítés a funkciók egy sorban, meg kell mutatnia, hogyan kell elvégezni közelítő értékek kiszámítása során a funkciókat hatványsorok.

Például, kiszámítjuk a közelítő értéke e ^ 0,1. Ezek a problémák könnyen megoldható nélkül kalkulátor segítségével bővítése a hatványsor.

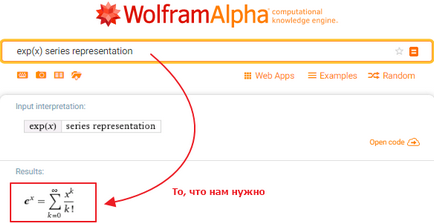
Meg kell szereznie a terjeszkedés e ^ x a hatványsor. Ehhez használjuk a megszokott kérés:

Minden, amit tudni akartál a pi szám, de nem merted megkérdezni, mert nem voltunk benne biztosak, hogy mit fognak mondani - ez az, amit szeretek hívni ezt a bejegyzést. Remélem, ha elolvassa a szöveget, hogy a végén, akkor nem lesz több kérdése a pi szám.

Kezdés egyszerű.

Az átlagember (nem matematika) érdekeltek lehetnek a szimbólum Pi. nevezetesen, hogy hogyan kell írni ezt a görög betű. De a webmester vagy programozó, továbbá szükség lehet információt a kódolt jel Pi különböző nyelvek és programozási rendszereket (így tettem a görög karakterkészlet π a címben ez a post). Mindkét esetben a segítségkérés:

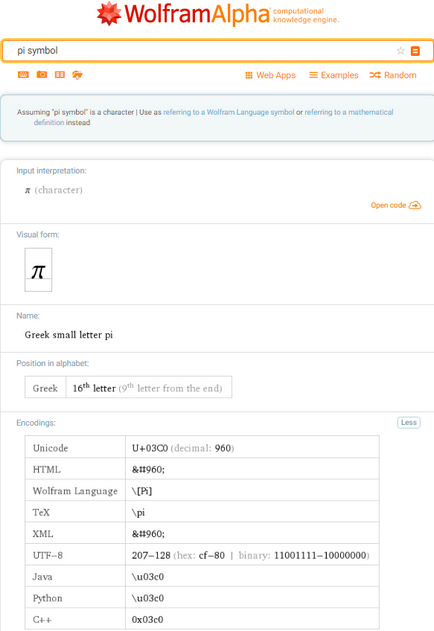
Ugyanaz a lekérdezés megmutatja, hogyan kell megtalálni a szimbóluma Pi különböző számítógépes billentyűzet (a görög nyelvet). A képernyő alján kimeneti kapjuk: