WolframAlpha orosz hogyan lehet bővíteni a függvény Fourier-sor
Hogyan lehet bővíteni a függvény Fourier-sor
A bővítés a funkciók Fourier használják elég gyakran, mert ebben a formában célszerű megkülönböztetni, integrálni, használja az eltolás érv a funkció, és a konvolúció funkciókat. Annak ellenére, hogy az eljárást a bővítés a Fourier-sor, még a legegyszerűbb esetben is meglehetősen időigényes, a rendszer Wolfram Alpha, mint általában, könnyen megbirkózni ezzel a feladattal.
Képviselteti magát a Fourier-sor trigonometrikus és exponenciális (komplex) formájában:
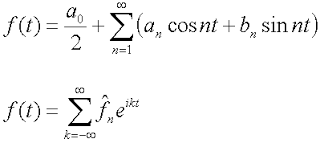
Az első kiviteli alaknál, mint az alapjául bomlás rendszert használnak Sines és koszinuszok. De ha dolgozik Fourier sorozat helyett sokkal kényelmesebb használni a kitevő egy képzeletbeli érv. Úgy tűnik tehát, Wolfram Alpha előnyös a második lehetőséget.
A legegyszerűbb módja annak, hogy bővítse a funkció Fourier-sor - küldjön egy kérést, mint Wolfram Alpha Fourier [függvényargumentumot a kifejezések száma a sorozat]. Például,
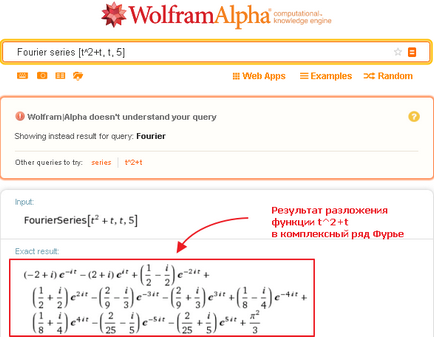
A kapott eredményeket szükség szerint benyújtott feltételeinek bővítése 5. szoba is beleértve; együtthatók a kitevővel fok konjugátum komplex konjugált számokat.
Egyidejűleg Wolfram Alpha nyújt grafikus ábrázolása a közelítése egy adott funkció Fourier-sor (itt, a központi része a grafikon megközelíti egy előre meghatározott parabola):
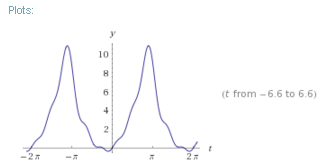
Még konkrétabban egyértelműen Fourier közelítése látható eredményei ezt a lekérdezést (amely közelíti egyenes Fourier-sor):
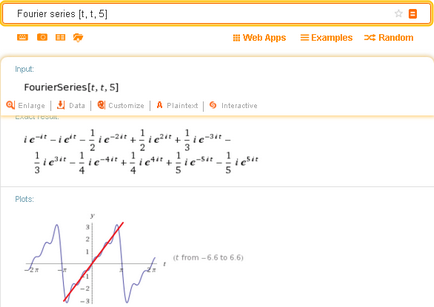
Bevezetés Egy adott funkció egy Fourier-sor trigonometrikus formában jelenik meg a legalsó része kérdés (itt - a második példa):
By the way, annak ellenére, hogy a fenti kérdés volt a rendszer: „Wolfram | Alpha nem érti Ön keresett következő helyett eredményeket keresett :. Fourier” - ami azt jelenti: „A rendszer nem érti a kérést mutatja az eredmények megfelelnek a lekérdezés: Fourier. „nem átverjék vele;) kérésre” Fourier”, amely azt javasolja, hogy a rendszer használatához, visszavonásra kerül, vagy életrajzi információkat matematikus Jean-Baptiste-Joseph Fourier (matematikus). Fourier-transzformáció a Fourier függvény [t ^ 2 + t]; attól függően, hogy tegye a szó „Fourier”, és közrefogják a rés, vagy sem.
Ha a kérelem nem határozza meg a Fourier sorfejtés egyértelműen a tagok száma n, akkor a rendszer Wolfram Alpha alapértelmezett kijelzők négy lehetőséget n 0-3, és csak a komplex formában a Fourier sor:
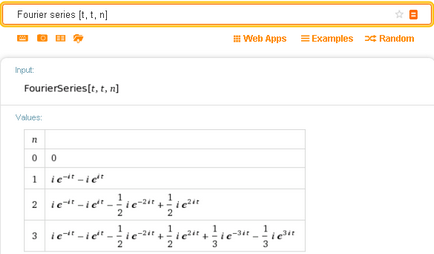
További lehetőségek bővítése n nagyobb, mint 3 nyerhető azonnal a „Tovább” gombra. De ez csak a grafikus ábrázolása az eredményeket:
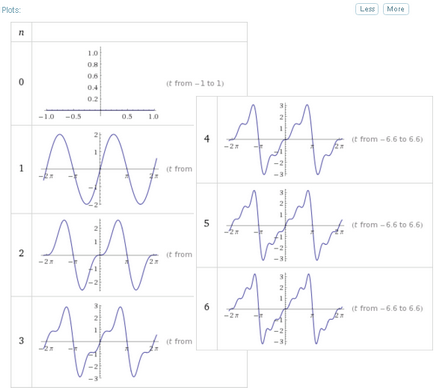
Így kapjuk a bomlási funkciók trigonometrikus Fourier, meg kell kérni Fourier határozza meg kifejezetten a kifejezések száma a bővítés.
Mi a teendő, ha a feladat nem az, hogy megtalálják a Fourier-együtthatóit a Fourier sor?
Először is, akkor FourierCoefficient kérelem [kifejezés érv, n]. amelyben Wolfram Alpha rendszer kimenetén az n-edik tágulási együtthatója expressziót a komplex Fourier-sor.
Például, az 5. expressziós tágulási együtthatója (t ^ 2 + t) Fourier-sor lehet a következőképpen állítjuk elő:
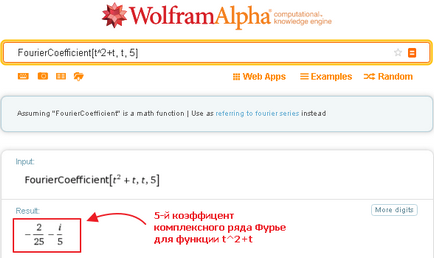
Ha azonban nem határozza meg kifejezetten n, akkor a lekérdezés fog mutatni egy általános kifejezés az N-edik együtthatója a Fourier-sor kifejezések:
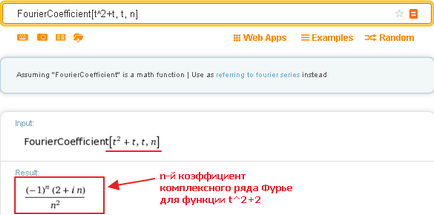
Ezen túlmenően, Wolfram Alpha majd egy táblázat, mint egy sor komplex Fourier-együtthatók (akár 15-ik távú, befogadó, ha rákattint az „Egyebek”):
Ebben a rövid áttekintés, én nem beszélve, hogy bővíteni a funkciót a Fourier-sor szinusz és koszinusz, vagy hogyan kell használni a számológépet Fourier Systems Wolfram Alpha, és nem szólt semmit a kétdimenziós Fourier-sorozat. Mindez - a téma a jövőm üzenetét. Tartsd szemmel a blog.