Személyes oldal - szinusz, koszinusz, tangens

Szinusz, koszinusz, tangens, kotangensét hegyesszög. Trigonometrikus függvények.

Sine a hegyesszög α a derékszögű háromszög - az aránya a másik lábát a átfogója.
Jelöljük: sin α.

Koszinusza hegyesszög α a derékszögű háromszög - az aránya a szomszédos láb a átfogója.
Jelöljük: cos α.

A tangense hegyesszög α - az aránya az ellenfél lábát, hogy egy szomszédos láb.
Jelöljük így: tg α.

Kotangensét hegyesszög α - az az arány a szomszédos egy másik lábát.
Jelöljük: CTG α.

Szinusz, koszinusz, tangens és kotangensét szög függ csak a szöget.

Leg b. közbezárt szög α, egyenlő a terméket átfogója sin α:

Lábát egy. szomszédos szög α, egyenlő a terméket átfogója cos α:

Leg b. szemközti sarkában α, egyenlő a terméket a második szár a tg α:

Lábát egy. szomszédos szög α, egyenlő a terméket a második szár a CTG α:

cos (90 ° - α) = sin α

Legyen egy négyszögletes ABC háromszög
AB = 6,
BC = 3,
szög = 30 °.

Nézzük sine a szög és a koszinusz a szög B.

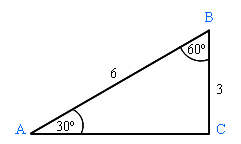
1) Először is, az a szög, B. Minden egyszerű: mint egy derékszögű háromszög egyenlő az összege akut szögek 90 °, a B szög = 60 °:

In = 90º - 30 ° = 60 °.

2) számoljuk sin A. Tudjuk, hogy a szinusz az arány a másik lábát, hogy az átfogó. Az a szög, és az ellenkező oldalon van az oldalán a Nap Tehát:

BC január 3
sin A = - = - = -
AB június 2

3) Most számoljuk cos B. Tudjuk, hogy a koszinusz az arány a szomszédos láb átfogója. A szög a szomszédos oldalán még mindig ugyanazon az oldalon a nap. Ez azt jelenti, hogy mi vagyunk ismét kell osztani a nap az AB - azaz, hogy ugyanazokat a lépéseket, mint a számítás sine a szög:

BC január 3
cos B = - = - = -
AB június 2

Az eredmény:
sin A = cos B = 1/2.

sin 30 ° = cos 60 ° = 1/2.

Ebből az következik, hogy egy derékszögű háromszög sine egy hegyesszög egyenlő a koszinusz a hegyesszög a másik - és fordítva. Ez mit jelent a két képlet:
sin (90 ° - α) = cos a
cos (90 ° - α) = sin α

Megmutatjuk, ezt még egyszer:

1) Legyen α = 60 °. Behelyettesítve a értéke α a képletben a szinusz, kapjuk:
sin (90 ° - 60 °) = cos 60 °.
sin 30º 60º = cos.

2) Legyen α = 30 °. Behelyettesítve a értéke α a koszinusz képletű, kapjuk:
cos (90 ° - 30 °) = sin 30 °.
cos 60 ° = sin 30 °.