Származékos példákat megoldások

előző ◈ a következő

Keresse időközönként növekedését és csökkenését, szélsőséges funkciók:

$Származékos példákat megoldások$

Ahhoz, hogy megtalálja a kritikus pontok megtalálják a leszármazottja az eredeti funkciót, és állítsa nullára.

$Származékos példákat megoldások$

Származtatott eltűnik a pont

$Származékos példákat megoldások$

A módszer alkalmazása az intervallumok előjele határozza meg a derivatív a mindenkori időközönként.

Származékos példákat megoldások

Így funkció növekszik

$Származékos példákat megoldások$

és csökkenti a

$Származékos példákat megoldások$

Szélsőséges funkciók:

$Származékos példákat megoldások$

a maximális pontot,

$Származékos példákat megoldások$

a minimális pontot.
Függvény értékei a szélsőérték:

$Származékos példákat megoldások$

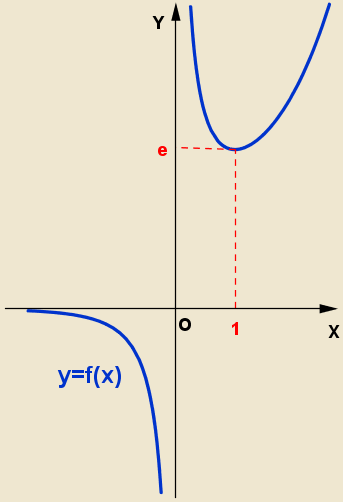
Ábrázolja a külleme:

Származékos példákat megoldások

Keresse időközönként növekedését és csökkenését, szélsőséges funkciók:

$Származékos példákat megoldások$

Ez a funkció definiálva

$Származékos példákat megoldások$

Kiszámítjuk annak származékai találni a kritikus pontokat és időközönként állandó jele a származék.

$Származékos példákat megoldások$

Figyeljük meg, hogy pont

$Származékos példákat megoldások$

és környékén az eredeti funkciója nem létezik.
Annál a pontnál

$Származékos példákat megoldások$

nincs eredeti funkcióját, vagy annak származéka. Így

Származékos példákat megoldások

Így funkció növekszik

$Származékos példákat megoldások$

és csökkenti a

$Származékos példákat megoldások$

Extremum a funkció:

$Származékos példákat megoldások$

maximális pontot. A függvény értéke ezen a ponton:

$Származékos példákat megoldások$

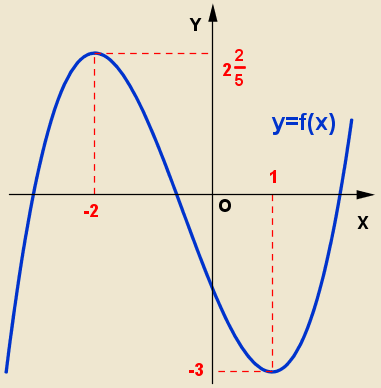
Ábrázolja a külleme:

Származékos példákat megoldások

Keresse időközönként növekedését és csökkenését, szélsőséges funkciók:

$Származékos példákat megoldások$

Ez a funkció definiálva

$Származékos példákat megoldások$

Kiszámítjuk annak származékai találni a kritikus pontokat és időközönként állandó jele a származék.

$Származékos példákat megoldások$

A kritikus pont

$Származékos példákat megoldások$

És azon a ponton

$Származékos példákat megoldások$

eredeti funkcióját, mind annak származéka nem létezik,
és pont

$Származékos példákat megoldások$

származék eltűnik. Az általunk használt intervallum módszert találni a származtatott jel
megfelelő időközönként.

Származékos példákat megoldások

Így funkció növekszik

$Származékos példákat megoldások$

és csökkenti a

$Származékos példákat megoldások$

Extremum a funkció:

$Származékos példákat megoldások$

a minimális pontot. A függvény értéke ezen a ponton:

$Származékos példákat megoldások$

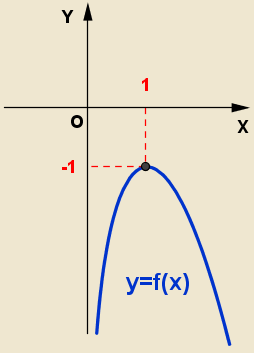
Ábrázolja a külleme:

Származékos példákat megoldások

előző ◈ a következő