Pitagorasz-trigonometrikus azonosság

By következménye 2, tangens és koszinusza azonos szögben kapcsolódnak szerint:

Fejezzük koszinusza meg:

Behelyettesítve ebben az egyenletben a beállított értéket, azt kapjuk,

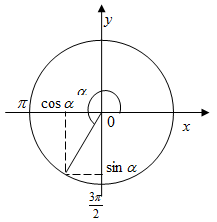
Ezzel együtt jár az első fő trigonometrikus azonosság

Annak megállapításához, a jelei a szinusz és koszinusz használatára további feltételek. Mivel tehát a szög fekszik a harmadik negyeddel (ábra. 4), van negatív koszinusz és szinusz. Aztán végül, megkapjuk

Mi azonnal megtalálja az érintő:

By következménye 2. alap trigonometrikus azonosságok, kotangensét és szinusz kapcsolja össze:

Fejezzük belőle sine:

Behelyettesítve Ebben az egyenletben a beállított értéket, azt kapjuk,

Az első fő következménye trigonometrikus azonosságok,

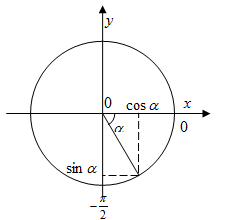
Annak megállapításához, a jelei a szinusz és koszinusz használatára további feltételek. A szög tartományban van ezért tartozik a negyedik negyedévben (5.), Van egy pozitív a sinus és cosinus negatív. Végül kap