Megoldása rendszerek lineáris egyenletek, a Gauss-Jordan

Általában a lineáris egyenlet:

Az egyenlet van egy megoldás: ha legalább az egyik együtthatók az ismeretlenek nem nulla. Ebben az esetben minden dimenziós vektor úgynevezett egyenlet megoldása, ha egyenlet azonosság helyettesítette koordinátáit.

Általános jellemzői a rendszer felbontása egyenletek

Jellemzésére az egyenletrendszert.

1. része a lineáris egyenletrendszer ellentmondásos egyenlet? (Ha az együtthatók, ebben az esetben, az egyenletnek formájában, és az úgynevezett inkonzisztens.)

• Ha a rendszer tartalmaz ellentmondásos, hogy egy ilyen rendszer következetlen, és nincs megoldás

2. Keresse meg a megengedett változókat. (Ismeretlen nazyvaetsyarazreshennoy a rendszert, ha van befoglalva egy egyenletrendszer együtthatóval +1, és a többi egyenletet nem tartalmazza (azaz, belép egy faktor nullával egyenlő).

• Példánkban az ismeretlen része az első egyenlet együttható egység, a második egyenlet nem tartalmazza, azaz először hagyjuk.
• Hasonlóképpen - már csak a második egyenletben, és csak az első.

3. Az engedélyezési rendszer egyenletek? (A rendszer egyenletek úgynevezett engedélyezett. Ha minden egyenlet tartalmaz engedélyezett ismeretlen, amelyek között nincs átfedés)

• Rendszerünk azért lehetséges, mert Minden egyenlet tartalmaz engedélyezett ismeretlen)

Megengedett ismeretlen vett egy-egy egyenletet a rendszer, alkossanak meg az engedélyezett ismeretlen rendszert. (Ebben a példában)

Megengedett ismeretlenek előforduló egy komplett, más néven az alapvető (), nem szerepel a beállított - free ().

Általában a felbontás az egyenletrendszer a következő formában:

Ebben a szakaszban a legfontosabb dolog, hogy megértsük, mi engedélyezett ismeretlen (részben az alapja és ingyenes).

Összesen Private alapvető megoldás

Az általános megoldás a rendszer engedélyezett gyűjteménye kifejezések engedélyezett ismeretlen a szabad feltételek és a szabad ismeretlenek:

Egy különösen oldatot a rendszer a megoldást, ami az általános az adott értékeket a szabad változók és ismeretlenek.

A bázikus oldatot nevezzük egy adott oldat, eredő teljes nulla értékek a szabad változók.

• Basic oldatot (vektor) nevezzük degenerált. ha a szám annak eredetét, nullától eltérő, kisebb, mint a megengedett számát ismeretlen.
• Basic megoldás az úgynevezett nem-degenerált. ha a szám annak eredetét, nullától egyenlő a megengedett számát ismeretlen rendszer tartalmazza a teljes készlet.

Tétel (1)

Megengedett egyenletrendszer mindig konzisztens (mert legalább egy megoldás); és ha a rendszer nem mentes az ismeretlennel (azaz az egyenletrendszert tartalmazza az összes beengedett alapján) definíció (egyedi megoldás); ha van legalább egy szabad változó, akkor a rendszer nem definiált (végtelen sok megoldás).

1. példa keresse meg az általános, alapvető, és bármely adott oldatát az egyenletrendszert:

1. Ellenőrizze, hogy a rendszer felbontása?

• A rendszert hagyjuk (például minden egyes egyenletek tartalmaz engedélyezett ismeretlen)

2. tartalmazza a szett engedélyezett ismeretlen - mindegyik egyenlet.

• A mi esetünkben, tudjuk felvenni a sor engedélyezett ismeretlen az első egyenletből - és mint a második egyenletből csak. Ez azt jelenti, egy sor állhat () és ().

3. Írja fel az általános megoldás, attól függően, hogy milyen jogosultságokat ismeretlen, már tartalmazza a készlet.

• mondjuk van benne egy sor ismeretlen, majd az általános megoldás nézne ki:

4. Keresse meg az adott megoldást. Ehhez azonosítjuk a szabad változók, hogy nem szerepel a beállított, hogy egyenlőségjelet egy tetszőleges számot.

• Tegyük fel, akkor az általános megoldás talált:

Válasz: A különösen oldatot (egy)

5. Mi található a lúgos oldat. Ehhez azonosítjuk a szabad változók, hogy nem szerepel a beállított nulla.

Elementary lineáris transzformációs egyenletek

A lineáris egyenletrendszer megengedett, hogy egyenértékűek a rendszerek elemi transzformációk.

Tétel (2)

Ha bármelyik rendszer egyenletet szorozzuk egy nem nulla szám. és a fennmaradó egyenletek változatlanok maradnak, megkapjuk a rendszer egyenértékű ezt. (Azaz, ha megszorozzuk a bal és a jobb oldalon az egyenlet azonos számú kapsz egy egyenletet egyenértékűek ezen)

Tétel (3)

Ha bármilyen egyenlet a rendszer bővíthető. és az összes többi egyenlet változatlan marad, megkapjuk a rendszer egyenértékű ezt. (Vagyis, ha hozzátesszük a két egyenletet (összegezve a bal és jobb oldalán), akkor megkapjuk az egyenlet egyenértékű adat)

Velejárója elmélet (2 és 3)

Ha bármilyen egyenletet újabb szorozva néhány számot. és az összes többi egyenlet változatlan marad, megkapjuk a rendszer egyenértékű ezt.

Képlet újraszámítása együtthatók

Ha van egy egyenletrendszert, és szeretnénk átalakítani, hogy egy egyenletrendszer lehetővé tette számunkra, hogy segítsen ebben módszer Gauss-Jordan.

Transzformálása Jordan megengedő elem előállítását teszi lehetővé egyenletrendszert az ismeretlen egyenlet tette a szobát. (2. példa).

Transzformálása Jordan áll elemi transzformációk két típusa van:

1. Egyenlet megengedő elem van osztva az említett elem által (szorozva)
2. Egyenletben megengedő elem szorozni egy megfelelő tényező, és hozzáadjuk a többi egyenletet, hogy megszüntesse az ismeretlen.

Tegyük fel, hogy azt akarjuk, hogy az ismeretlen, az alsó egyenletben engedélyezett ismeretlen. Ehhez meg kell osztani, úgy, hogy az összeg.

2. példa újraszámítja az együtthatók

Amikor elosztjuk az egyenlet a számot a koefficiensek újraszámítja képletek szerint:

kizárása

egyenletből index , Szükségünk van egy egyenlet számos szorozva és hozzáadjuk az egyenlet.

Tétel (4), hogy csökkentse a számú egyenlet.

Ha a rendszer az egyenletek tartalmazza a triviális egyenlet, azt ki lehet küszöbölni a rendszerből, így olyan rendszert egyenértékű az eredeti.

Tétel (5) A összeférhetetlenségét egyenletek.

Ha az egyenletrendszert ellentmondásos egyenlet, ez ellentmondásos.

Az algoritmus a módszer Gauss-Jordan

Az algoritmus megoldására egyenletrendszer a Gauss-Jordan áll egy sor hasonló lépéseket, amelyek mindegyike végez műveleteket ebben a sorrendben:

1. Jelölve, nem mond ellent a rendszer. Ha a rendszer tartalmaz egy ellentmondásos egyenlet, ez ellentmondásos.
2. Ellenőrizte a lehetőségét számának csökkentése egyenletek. Ha a rendszer tartalmaz egy triviális egyenlet, a sztrájk ki.
3. Ha az egyenletrendszert megoldódik, akkor írj az általános megoldás a rendszer, és ha szükséges - saját megoldásokat.
4. Ha a rendszer nem megengedett, akkor az egyenletben nem tartalmazó ismeretlen megengedett, amely lehetővé teszi a kiválasztott elem és termelnek konverziós Jordan ezzel a elemet.
5. További visszautalt az 1. bekezdés

3. példa Hogy oldja az egyenletrendszert a Gauss-Jordan.

Find. Két általános és két megfelelő lúgos oldatok

A számítások adott az alábbi táblázatban:

A jobb oldalon a táblázatban a műveleteket az egyenletek. Nyilak jelzik, amelyhez hozzáadjuk az egyenlet egyenlet megengedő elem megszorozva a megfelelő tényezővel.

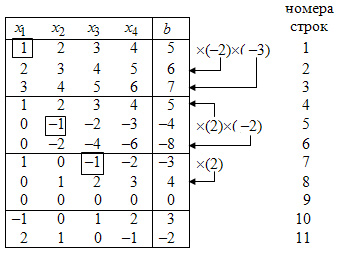
Az első három a táblázat sorai kerülnek az együtthatók az ismeretlen és a jobb oldalán az eredeti rendszer. Az eredmények az első átalakító elem Jordan megengedő egységét látható vonalak 4, 5 és 6. eredmények a második átalakító elem Jordan megengedő egyenlő (-1) mutatjuk be 7, 8 vezeték, 9. Mivel a harmadik egyenlet triviális, nem tud figyelembe kell venni.

Egyenértékű rendszer engedélyezett ismeretlen, a következő formában:

Most tudjuk írni az általános megoldás:

Mi egyenlőségjelet szabad változók, és a nulla és azt kapjuk.

Ahhoz, hogy megtalálja a második általános és a megfelelő alapvető megoldás, ami a rendszer felbontása semmilyen egyenlet akkor ki kell választania bármely más elemet, amely lehetővé teszi. (Az a tény, hogy a lineáris egyenlet tartalmazhat némi általános és alapvető megoldásokat). Ha a felbontás a egyenletrendszer ekvivalens az eredeti rendszer tartalmaz ismeretlenek és az egyenletek száma, a közös és a vonatkozó határozatai alapján az eredeti rendszer a kombinációk száma és. A kombinációk száma lehet képlettel számítottuk ki:

A mi esetünkben, mi kiválasztva, amely lehetővé teszi elem (1) az első egyenlet (7 sor). Következő az átalakulás Jordan. Kapunk egy új (vonalak 10-11) hagyjuk c új rendszer lehetővé tette ismeretlenek:

Írja be a második általános megoldás:

És a megfelelő lúgos oldat.