Lagrange multiplikátor módszer - studopediya

LP és NLP problémákat megoldani az 1 lépésben. Ilyen problémák nevezzük egylépéses (azonos típusú). Dean feladat. Pr. úgynevezett többlépcsős - minden lépésben határozza meg a határozat egyes részeinek feladatok miatt az eredeti probléma.

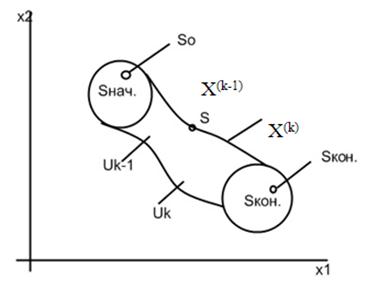
Az általános megfogalmazása a DP célkitűzések. Legyen egy fizikai rendszer S még kezdeti állapotban S0 Je Snach. és ez kezelhető. Köszönhetően egy kis mozgásra. U a rendszer mozog a kezdeti állapotból a végső állapot S0 Skon. Skon Je SK.

Így például az egyes vezérlők U jellemzi a megfelelő érték a függvény W (U).

A kihívás az, hogy megtudja, több ellenőrzés, amelyben a függvény W (U) úgy szélsőséges értéket.

DP problémamegoldás végezzük program keretében:

Feltételezzük, hogy az állam a figyelembe vett S rendszer, amelyen a k - m lépést, ahol k = 1 ... n kombinációja határozza meg a számok X (k) = (x1 (k) X2 (k) ... xn (k) ..), amely származnak uk eredményeként a vezérlő rendszer egy átmeneti Siz állapotban X (k-1), hogy az állami x (k).

Feltételezzük, hogy az állam X (k) állapotától függ X (k-1), és a kiválasztott kontroll Uk, de nem függ attól, hogy az S rendszer telt ebben az állapotban.

Metszés. Ahhoz, hogy végre az első lépést kaptunk erősítést állapotban függ dok. állapot (X (k-1)) és az Egyesült Királyságban egyenletet.

A teljes hozzájárulás ebben az esetben a következő lesz:

F = Σ Wk (X (k-1), Uk)

DP problémák megoldására ilyen rendszer keretében végzett elve optimalitást Bellmona.

Nyilatkozat: mi lett volna az állam a rendszert, mielőtt a következő lépés legyen a következő lépés az, hogy válassza ki a vezérlő, hogy a nyereség ebben a lépésben, valamint az optimális erősítést minden következő lépést maximális.