Komplex számok Válogatott problémák

Szövetségi Hivatal OKTATÁS

ÁLLAPOT Oktatási Intézmény

FELSÕOKTATÁSI

„Voronyezs Állami Pedagógiai Egyetem”

ELNÖK AGLEBRY és geometria

Végső minősítő munkák

A speciális 050.201,65 Matematika

(További különlegessége 050.202,65 informatika)

Teljesülnek: a hallgató 5. év

2. Komplex számok (kiválasztva problémák)

2.1. Komplex számok algebrai formában .... ....... .......... ....

2.2. A geometriai értelmezése komplex számok ............ .. ...

2.3. Trigonometrikus forma komplex számok

2.4. Alkalmazása az elmélet a komplex számok, hogy megoldja az egyenleteket a 3. és 4. fokú ............... .. ...............................................................

2.5. Komplex számok és paraméterek .......... ......................... ....

A program a matematika iskolai tanfolyamot számelmélet által bevezetett példát készlet természetes számok, egész számok, racionális, irracionális, azaz A valós számok halmazán, képek, amelyek teljes egészében kitölti a számegyenesen. De a 8. osztályos készletek a valós számok nem elég, Másodfokú egyenletek megoldása negatív diszkrimináns. Ezért szükséges, hogy pótolja az állomány valós számok komplex számok, amelyekre a négyzetgyök negatív szám van értelme.

A választás a téma „Komplex számok”, mint a téma az én végső minősítő munkája az a tény, hogy a koncepció egy komplex szám bővül tanulók tudását numerikus rendszerek megoldására széles osztály a problémák, mint az algebrai és geometriai tartalma megoldásának algebrai egyenletek bármilyen fokú és problémák megoldására paramétereket.

Ebben a dolgozat vizsgálta oldat 82 x célkitűzéseit.

Az első rész a főrész „komplex számok” olyan megoldások, hogy problémák komplex számok algebrai formában, meghatározott műveletek összeadás, kivonás, szorzás, osztás, kapcsolási művelet komplex számok algebrai formában, a mértéke az imaginárius egység, a modul a komplex szám, és leírja általában figyelembe véve a négyzetgyöke komplex szám.

A második részben a probléma megoldható egy geometriai értelmezése komplex számok vagy vektorok pont a komplex síkban.

A harmadik rész foglalkozik műveletek komplex számok trigonometrikus formában. Formula használt: Moivre és kivonása a gyökér a komplex szám.

A negyedik rész fordítják megoldása az egyenleteket a 3. és 4. évfolyamon.

A feladatok megoldásához az utolsó része a „Komplex számok és paraméterek” használják, és biztosította megadott adatok az előző részek. Heads feladatok sorozat elkötelezett a meghatározása családok sor a komplex síkban által meghatározott egyenletek (egyenlőtlenségek) paraméterrel. Ennek része a testmozgás kell megoldani az egyenletet egy paramétert (C felett). Vannak munkahelyek, ahol a komplex változó egyidejűleg kielégíti számos feltételnek. A jellemző problémák megoldására ebben a szakaszban, hogy csökkentse a legtöbbjük az egyenletek megoldása (egyenlőtlenségek, rendszerek) a másodfokú, irracionális, trigonometrikus, egy paramétert.

A funkció bemutatása anyag minden egyes része külön bemenet kezdeti elméleti alapjait, és ezt követően azok gyakorlati alkalmazása a problémamegoldásban.

Végén a dolgozat egy lista a felhasznált irodalom. Legtöbbjük meglehetősen részletes és a rendelkezésre álló felvázolja az elméleti tárgyalt néhány problémát, és megoldásokat kapnak gyakorlati feladatok önrendelkezés. Figyelemre méltó a forrásokból, mint például:

1. Gordienko NA Belyaeva ES Firstov VE Serebryakov IV Komplex számok és alkalmazásaik: tankönyv. [10]. Anyaga tankönyv formájában mutatják be az előadások és gyakorlati feladatok.

2. DO Shkliarsky NN Chentsov Yaglom IM Válogatott problémák és tételek az elemi matematika. Aritmetika és algebra. [21] A könyv 320 feladatokat tartalmaz releváns az algebra, és az elmélet a számtani számokat. Jellegüknél fogva ezek a kihívások jelentősen eltérnek a hagyományos iskolai feladatokat.

2. Komplex számok (kiválasztva problémák)

2.1. A komplex számok algebrai

A számos probléma megoldását a matematika, a fizika csökkenti a megoldás az algebrai egyenletek, azaz egyenletek formájában

,

ahol a0. a1. ..., an valós számok. Ezért a tanulmány az algebrai egyenletek egyik legfontosabb kérdés a matematikában. Például, az igazi gyökereit a másodfokú egyenlet nincs negatív diszkrimináns. A legegyszerűbb ilyen egyenlet egyenlet

.

Annak érdekében, hogy ez az egyenlet van egy megoldás, hogy ki kell terjeszteni a valós számok halmaza csatolásával rá a gyökere az egyenlet

.

Jelöljük ezt a gyökértől

. Így definíció szerint,

,

.

Felszólította az imaginárius egység. Vele, és egy pár valós számok

előkészített expresszióját formájában

.

A kapott expressziós az úgynevezett komplex számok, mivel tartalmazza mind a valós és a képzetes rész.

Így a komplex számok nevezzük kifejezések az űrlap

,

- valós szám, és

- jelképe kielégítő

Ez az úgynevezett valós része egy komplex szám

- képzetes része. Mert a használt megnevezések szimbólumok

,

.

Komplex számok formájában

Ezek valós számok, és ezért több komplex számok tartalmaz egy készlet valós számok.

Komplex számok formájában

úgynevezett tisztán képzetes. Két komplex számok formájában

azt mondta, hogy egyenlő, ha azok a valós és képzetes része, azaz ha az egyenletek

,

.

Algebrai bejegyzést komplex számok segítségével a műveleteket végrehajtó által rájuk az általános szabályok szerinti algebra.

Az összeget két komplex szám

komplex szám

.

.

Írása egy nem nulla komplex szám Z

Ez az úgynevezett trigonometrikus formájában komplex szám z. Az r szám úgynevezett modulus komplex szám Z, és a szám a # 966; ezt nevezik az érvelés egy komplex szám, és jelöljük Argz.

Trigonometrikus forma egy komplex szám - (Euler-képlet) - exponenciális formájának a komplex szám:

.

Egy komplex szám z végtelen sok érv: ha # 966; 0 - bármely érve z, akkor a többi megtalálható a következő képlet segítségével

.

Egy komplex szám

érv és trigonometrikus formában nem mutatható ki.

Ily módon a nem-zéró argumentum komplex szám

jelentése minden olyan megoldást a rendszer:

érték # 966; az érvelés egy komplex szám Z, kielégíti a egyenlőtlenségeket

, Ez az úgynevezett elsődleges és a kijelölt argz.

Érvek Argz és argz rokonságban

(5) a következménye, a rendszer (3), hogy minden érv a komplex szám

kielégítik az egyenlet (5), de nem az összes oldat # 966; (5) egyenlet a száma érvek z.

A fő értéke az érvelés nem nulla komplex szám

képlet adja meg:

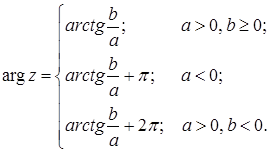
Formula szorzási és osztási komplex számok trigonometrikus formában a következők:

Amikor erecting egy természetes erejét a komplex szám használt Moivre képletű:

képletet használjuk, amikor kitermelése a gyökér a komplex szám: