Időközönként növekedését és csökkenését

A következő típusú funkciók monotónia:

1) funktsiyavozrastaet. Ha egy bizonyos időtartam, amennyiben ilyen birtokló bármely két pont, és ezt az intervallumot, hogy. Ie nagyobb értéke az érv felel meg egy nagyobb értéket a függvény;

2) funktsiyaubyvaet. Ha egy bizonyos időtartam, amennyiben ilyen birtokló bármely két pont, és ezt az intervallumot, hogy. Ie nagyobb értéke az érvelés megfelel a minimális érték a funkció;

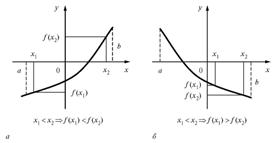
3) funktsiyaneubyvaet. Ha egy bizonyos időtartam, amennyiben ilyen birtokló bármely két pont az intervallum, és hogy;

4) funktsiyanevozrastaet. Ha egy bizonyos időtartam, amennyiben ilyen birtokló bármely két pont, és ezt az intervallumot, hogy.

2. Az első két esetben a „szigorú monotonitás” is alkalmazni kell.

3. Az utóbbi két esetben specifikusak, és általában szerint olyan készítmény, több funkciót.

4. Külön megjegyezzük, hogy fontolja meg a növelés és csökkentés menetrend funkciók pontosan a bal-jobb és semmi mást.

Ez a funkció a furcsa. Ha megváltoztatja a jel az az érv, hogy megváltoztatja annak értékét az ellenkezője. A képlet így néz ki ezt a bejegyzést. Ez azt jelenti, hogy miután a helyettesítés a függvény helyett minden X értékeit „mínusz X”, a függvény megváltoztatja jel. A grafikon ennek a funkciónak szimmetrikus az eredetét.

Ilyenek például a páratlan funkciókat, és mások.

Például, a grafikon nem rendelkeznek szimmetria a származás:

Ez a funkció a még. ha a megjelölés az érvelés változás, ez nem változik az értéke. A képlet így néz ki ezt a bejegyzést. Ez azt jelenti, hogy miután a helyettesítés a függvény helyett minden X értékeit „mínusz X”, a függvény eredményeként nem fog változni. A grafikon az ezt a funkciót szimmetrikus tengely körül.

Példák a még funkciók és mtsai.

Például, a grafika mutatják szimmetria tengelye körül:

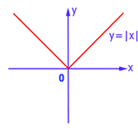
Ha a függvény nem tartozik semmilyen ilyen típusú, ez az úgynevezett akár páros vagy páratlan, vagy általános típusú funkciót. Ezek a funkciók nem szimmetrikus.

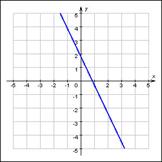
Ez a funkció például a közelmúltban az egyik általunk vizsgált lineáris függvénye a menetrend:

3. A különleges tulajdonságait funkciók a frekvencia.

Az a tény, hogy a periodicitás a funkciót, amelyek szerinte a standard tananyag, csak a trigonometrikus függvények. Már beszéltünk részletesen róluk a tanulmány az érintett témákban.

Periodicitás a funkció - egy funkció, amely nem változtatja meg az értékét oly módon, hogy az az érv egy bizonyos számú nem nulla konstans.

Ez a minimális számot hívják az időszakban a funkció és betűvel jelöljük.

A képlet ezt a rekordot a következő :.

Nézzünk egy példát az ingatlan egy szinusz görbe:

Emlékezzünk, hogy az idő a funkciók. és időszak -.

Mint már tudjuk, hogy a trigonometrikus függvények a komplex érv lehet egy nem szabványos időszakban. Beszélünk a funkciókat a formában:

Ezek időtartamával megegyező. És a funkciók:

Ezek időtartamával megegyező.

Mint látható, a számítás egy új időszak egy standard időszakra elosztják a tényező az érvelés. A másik változtatás funkció nem függ.

Egy függvény y = f (x) nevezzük határolja alulról egy sor H⊂D (f), ha van egy szám, és hogy minden x # 1013; x kielégíti az egyenlőtlenséget f (x)

Egy függvény y = f (x) nevezzük egy felső határt a beállított H⊂D (f), ha van egy szám, és hogy minden x # 1013; x kielégíti az egyenlőtlenséget f (x)

Ha X nem megadott időtartam, úgy tekinthető, hogy a funkció határolja saját domain. Funkciója korlátozott, valamint fent és lent az úgynevezett korlátos.

Korlátai funkció könnyen olvasható menetrend szerint. Tudod felhívni egy bizonyos vonalat y = a, és ha a funkció sor felett, majd alulról korlátos.

Ha alacsonyabb, illetve felülről. Az alábbiakban egy grafikon alatti korlátos függvény. Ütemezése korlátozott funkciójú, fiúk, próbálja festeni magukat.

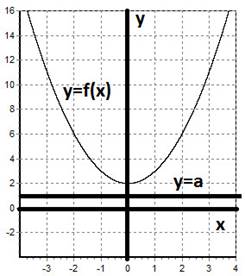
Tárgy: A tulajdonságok funkciók: időközönként növekedését és csökkenését; maximális és minimális értékek pont szélsőérték (helyi maximum vagy minimum), domború funkciót.

Időközönként növekedését és csökkenését.

Alapú elégséges feltételek (attribútumok) a növekedés és csökkenés funkciók időközönként növekedését és csökkenését funkciókat.

Itt látható a szövege jelei a növekvő és csökkenő függvény a:

· Ha a függvény deriváltját y = f (x) pozitív minden x a függvény X. intervallum megnő X;

· Ha a függvény deriváltját y = f (x) negatív minden x a függvény X. intervallum csökken X.

Így, hogy meghatározzák a időközönként növekedése és csökkenése a funkciót:

· Saját domain a funkció;

· Keresse meg a függvény deriváltját;

· Problémák egyenlőtlenségek és a domén;

· Hozzáadás keletkező hézagokat határ pont, amelynél a funkció határozza meg, és a folyamatos.

Tekintsük a példát a megállapítással, hogy egyre nagyobb időközönként, és csökken a függvény megmagyarázni az algoritmust.

Keresse időközönként növekedését és csökkenését a funkciót.

Az első lépésben meg kell találni a domain a funkciót. Példánkban a kifejezést a nevező nem lesz nulla, ezért.

Azt viszont, hogy megtaláljuk a származékot egy funkciót:

Annak megállapításához, a időközönként növekedés és csökkenés több mint elegendő alapot funkció megoldja az egyenlőtlenségek és a domain. Mi egy általánosítása intervallum módszer. Az egyetlen igazi gyökerei a számláló x = 2, és a nevező nulla lesz az x = 0. Ezek a pontok osztja a domain be időközönként, amelyekben a származék megtartja az aláírására. Megjegyezzük, hogy ezek pont a számegyenesen. A Be- és kimenetek hagyományosan jelölik időközönként, amelyek esetében a derivált pozitív vagy negatív. A nyilak az alábbiakban vázlatosan mutatják növelheti vagy csökkentheti a funkció a megfelelő intervallumban.

Így mind.

Azon a ponton, x = 2, a funkció határozza meg, és a folyamatos, azonban hozzá kell tenni, hogy a különbség, hogy növelje vagy csökkentse a rés. Azon a ponton, x = 0 nincs meghatározva, ezért nem tartalmazzák ezt a pontot a kívánt intervallumokban.

Itt a menetrend függvényében az összehasonlítás velük az eredményeket.

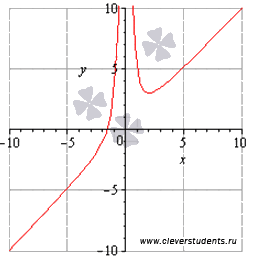
A: A funkció növekszik. csökken a (0, 2].