Hogyan lehet megtalálni az irányt az alapja a piramis
Kihívások számításának alapja a piramis a probléma könyv geometria meglehetősen nagy részén. Sok függ attól, hogy mit gemoetricheskaya alak fekszik a bázis, valamint attól, amit megadott a problémát.
szüksége lesz
- - rajzkellékek;
- - könyv a ketrecben;
- - szinusz;
- - Pitagorasz-tétel;
- - számológép.
oktatás
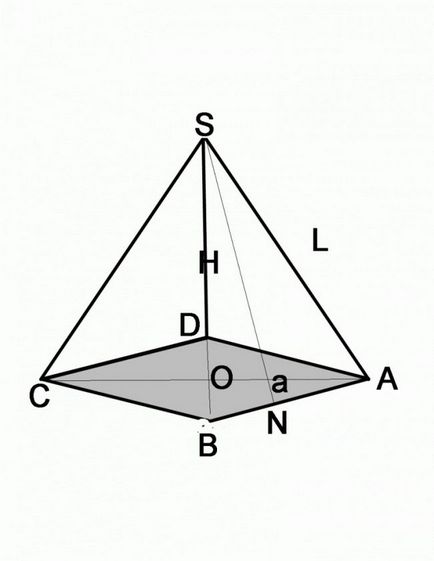
Az iskolában geometria természetesen elsősorban foglalkozik a piramis alján, amely egy szabályos sokszög, hogy van, amelyben minden fél egyenlő. A vetítés a csúcsa a piramis egybeesik a központ az alap. Rajzolj egy piramis, amelynek alapja egy egyenlő oldalú háromszöget. A feltételeket adható:
- hossza oldalélei a piramis, és annak szöget közötti él az oldalsó felület és osnovaniem-
- hossza oldalszélei és egy oldalsó magassága bounda-
- hosszát és magasságát az oldalsó szélei a piramis.
Ha tudja, hogy az oldalsó széle és a szög, a probléma megoldódik némileg eltérő. Emlékezzünk, hogy mindegyik egy oldallapja a piramis, amelynek alapja egy egyenlő oldalú sokszög. Ez egy egyenlő szárú háromszög. Töltsön magassága, amely szintén a felezővonal, a medián. Azaz, a bázis oldalán fél / 2 = L * cosa, és ahol - a bázis oldalán a piramis, L - szegély hossza. Ahhoz, hogy megtalálja a méret a bázis oldalán, elég az eredményt megszorozzák 2.

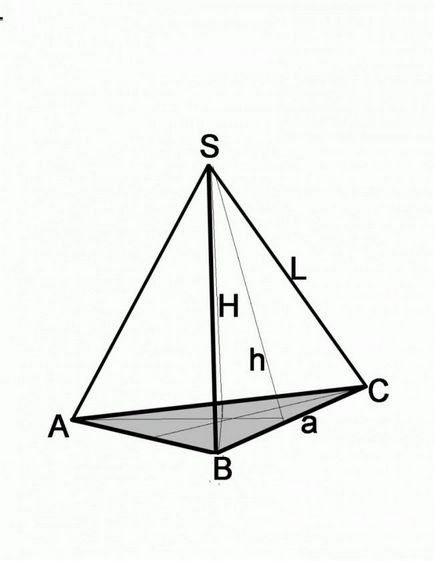
Ha a probléma adott a magassága az oldalsó felületek és élek hossza, hogy az alap felé a Pitagorasz-tétel. Oldallap ebben az esetben az átfogója ismert magasságú -s egyik lábát. Ahhoz, hogy megtalálja a hossza a második láb, meg kell kivonni a tér a átfogója négyzetes második láb, vagyis (A / 2) 2 = L2-h2, ahol egy - az alap egyik oldalán, L - a hossza az oldalsó felület, h - a magassága az oldalsó felület.
Ebben az esetben el kell végezni a további építési, hogy képes legyen működtetni a trigonometrikus függvények. Ön adni a oldaléle L és H magassága a piramis, amely összeköti a tetején a piramis a bázis központja. A magassága a metszéspontja a sík a bázis végezzen szegmens összekötő, hogy pont az egyik az alap sarkait. Most már derékszögű háromszög, átfogója amely az oldalsó éle az egyik lábát - a magassága a piramis. Ezen adatok szerint könnyű megtalálni a második szakasz a háromszög, elég egy négyzet tálalószekrény L vonjuk ki a megadott testmagasság négyzetének H. Ami ezután történik, attól függ, milyen alakú az alapja.
Ne feledje, a tulajdonságok egy egyenlő oldalú háromszög. Ez a magasság bisectors és a középső. A kereszteződésekben, ők osztják ketté. Azaz, kiderül, hogy megtalálta a fele a magassága az alap. Az egyszerűbb számítás elvégzésére mindhárom magasságokba. Látni fogja, hogy a szegmens, négyzet, amelynek hossza már megtalálta, az átfogó egy derékszögű háromszög. Távolítsuk el a négyzetgyök. Tudja, és hegyesszög - 30 °, hiszen ez a megállapítás a fele az alap nem lesz nehéz, a koszinusz tétel.
Mert piramisok amelynek alapja a rendszeres négyszög, az algoritmus ugyanaz lenne. Ha vonjuk ki a tér a szélei a tér magassága a piramis, hogy négyzet bázis fele átlósan. Vegye ki a gyökér, hogy az átlós mérete, ami szintén a átfogója egy egyenlő szárú derékszögű háromszög. A méret minden a lábak, hogy a Pitagorasz-tétel, sinus, vagy cosinus.