Hogyan lehet megtalálni a kerülete és területe a kör

Kör - egy sima zárt görbe, melynek pont egyenlő távolságra van a középponttól. [1] kerülete (C) - a hossza egy zárt görbe, amely egy kör. [2] A terület egy kör (A) - olyan intézkedés a tér által körülhatárolt kör. [3] A terület a kör, és a kerülete számítjuk képletek szerint, amelyben van egy sugár (vagy átmérőjű) a kör és a szám a „pi”.

lépések szerkesztése

1. rész 3: számítása a kerülete szerkesztése

A képlet kiszámításához kerületi hossza. Kerületi hossza lehet kiszámítani két képlet: C = 2πr vagy C = πd, ahol π - szám „pi” (matematikai állandó megközelítőleg egyenlő 3,14) [4]. r - a kör sugarát, d - a kör átmérője. [5]

• A fenti képlet lényegében ugyanaz, mivel az átmérő kétszerese a sugara.
• A kerülete mérjük minden egység hossza: méterben, centiméter, milliméter, és így tovább.

Értékei formula. A képlet a megállapítás a kerülete Három érték: a sugár, átmérőjét és számát „pi”. A sugár és átmérő kapcsolódik egymáshoz: a sugár egyenlő átmérő fele, és az átmérő kétszerese a sugár.

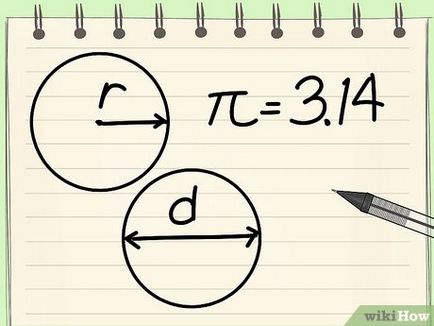
• Sugara (R) - egy összekötő szakasz közepén a kör bármely pontjára a kör.
• kör átmérője (d) - egy szegmens közepén áthaladó kör és csatlakozik a két pont a kör. [6]
• A számos „pi» (π) egyenlő az arány a kerülete és átmérőjének; a szám a „pi” irracionális szám, ami nagyjából megegyezik a 3.14159265 és véges számok, és az ismétlődő számok kombinációjaként. [7] A legtöbb matematikai számítások száma „pi” van kerekítve 3,14.

Mérjük meg a sugár vagy a kör átmérője. Igazítsa a vonalzó bármely pontjára a kör és győződjön meg róla, hogy a vonal érintkezik a közepén a kör. Mérjük meg a távolság a pont a közepén a kör, így az érték a sugár. Mérjük meg a két pont közötti távolság feküdt egy kört kapunk egy értéket az átmérője.

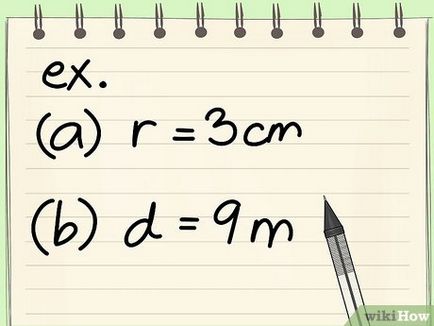
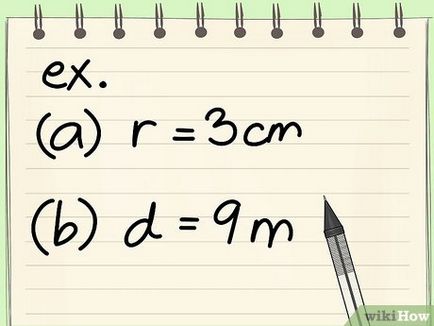
• A legtöbb matematikai problémák sugár vagy átmérő kap.

Helyettesítsük az értékeket a formula. Megtalálása a sugár és / vagy a a kör átmérője, hogy helyettesítse a értéket egy megfelelő általános képletű. Ha úgy találja, a sugár, akkor a képlet C = 2πr, és ha az átmérője a képlet C = πd.

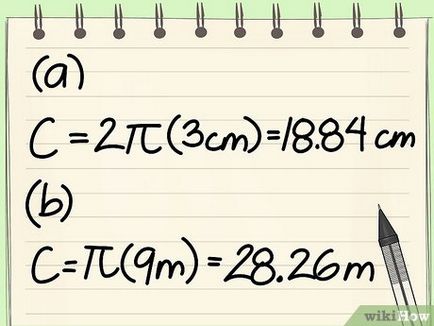
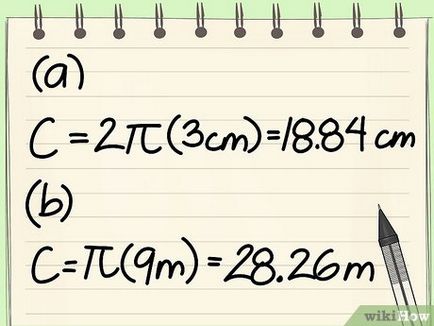
• Példa: kap egy kerülete, amelynek sugara egyenlő 3 cm.
  • Write képlet: C = 2πr
  • Helyettesítse ezt az értéket a képlet: C = 2π3
  • Szorzás: C = (2 * 3 * π) = 6π = 18,84 cm
• Példa: kap egy kerülete, amelynek átmérője 9 m.
  • Write képlet: C = πd
  • Helyettesítse ezt az értéket a képlet: C = 9π
  • Szorzás: C = (9 * π) = 28,26 m

Gyakorlat néhány példát. Most, hogy tudod, hogy a formula, próbálja megoldani számos problémát. A több problémát megoldani, annál gyorsabban megtanulják, hogyan kell kezelni őket.

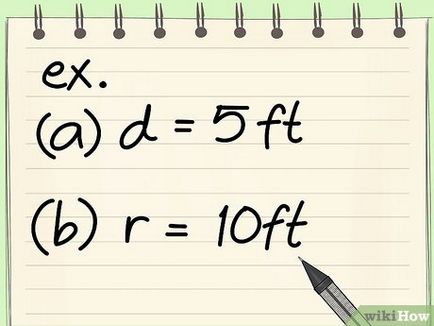
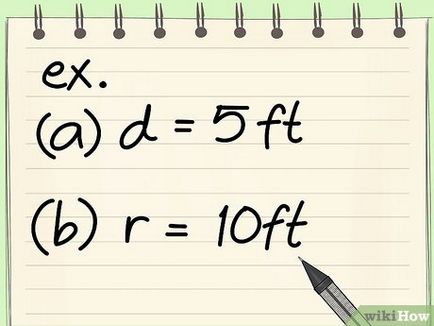
• Keresse kerületi hossza egy 5 m átmérőjű.
  • C = πd = 5π = 15,7 m
• Keresse kerületi hossza sugarú 10 m.
  • C = 2πr = C = 2π10 = 10 * 2 * π = 62,8 m

2. rész 3: számítsa ki a terület a kör szerkesztése

A képlet a terület a kör. terület egy kör segítségével számítható két képlet, amely tartalmazza az átmérő vagy a sugár: A = πr 2 vagy A = π (d / 2) 2 [8]. ahol π - szám "pi" (matematikai állandó megközelítőleg egyenlő 3,14) [9]. r - a kör sugarát, d - a kör átmérője.

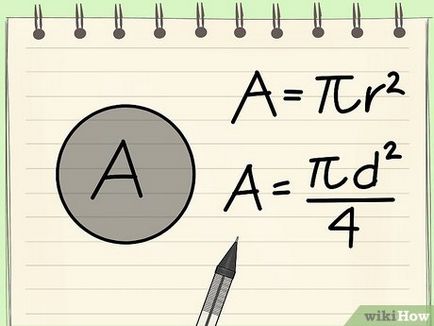
• A fenti képlet lényegében ugyanaz, mivel az átmérő kétszerese a sugara.
• terület egy kör mérjük minden egység hosszúságú, négyzetes: négyzetméterben (m 2) négyzetcentiméterben (cm 2) négyzetmilliméterben (mm 2), és így tovább.

Értékei formula. A képlet megtalálására a terület a kör magában foglalja három érték: a sugár, átmérőjét és számát „pi”. A sugár és átmérő kapcsolódik egymáshoz: a sugár egyenlő átmérő fele, és az átmérő kétszerese a sugár.

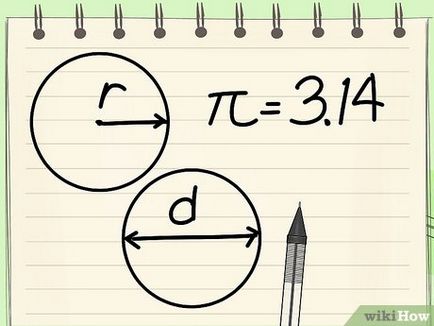
• A sugár (R) - egy összekötő szakasz közepén a kör bármely pontjára a kör, amely meghatározza a kört.
• Kör átmérője (d) - egy szegmens közepén áthaladó kör és csatlakozik a két pont a kerületén, amely korlátozza a kör. [10]
• A számos „pi» (π) egyenlő az arány a kerülete és átmérőjének; a szám a „pi” irracionális szám, ami nagyjából megegyezik a 3.14159265 és véges számok, és az ismétlődő számok kombinációjaként. [11] A legtöbb matematikai számítások száma „pi” van kerekítve 3,14.

Mérjük meg a sugár vagy a kör átmérője. Igazítsa a kezdő felállás minden korlátozó pont a kör kerületének, és győződjön meg róla, hogy a vonal érintkezik a közepén a kör. Mérjük meg a távolság a pont a közepén a kör, így az érték a sugár. Mérjük meg a két pont közötti távolság feküdt egy kört kapunk egy értéket az átmérője.

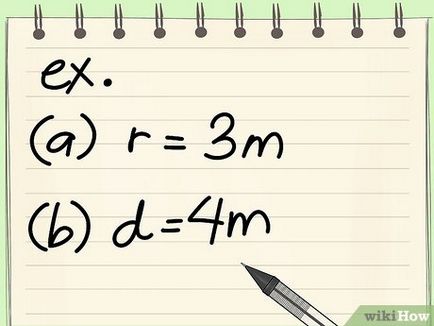
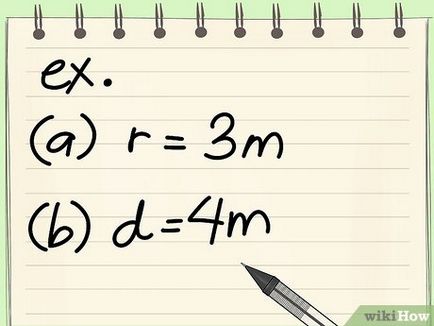
• A legtöbb matematikai problémák sugár vagy átmérő kap.

Helyettesítsük az értékeket a formula. Megtalálása a sugár és / vagy a a kör átmérője, hogy helyettesítse a értéket egy megfelelő általános képletű. Ha úgy találja, a sugár, akkor a képlet = πr 2. És ha az átmérő képlet A = π (d / 2) 2.

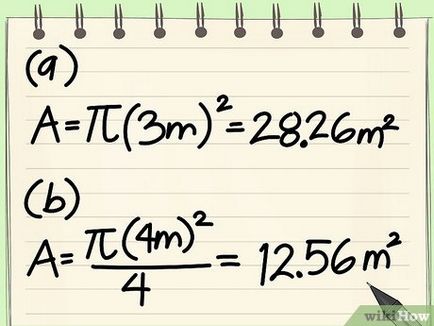
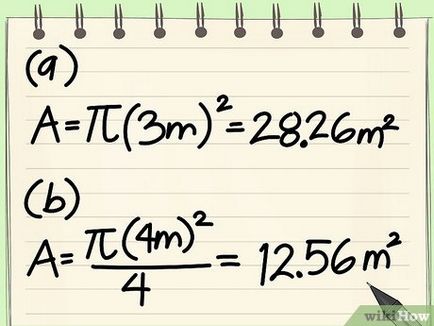
• Példa: kap a terület egy kör sugara 3 m.
  • Írja képlet: A = πr 2
  • Helyettesítse ezt az értéket: A = π3 2
  • Lift sugarának négyzetével: r 2 = 3 2 = 9
  • Szorozzuk száma „pi»: A = 9π = 28,26 m 2
• Példa: kap a terület egy kör átmérője 4 m.
  • Írja képlet: A = π (d / 2) 2
  • Helyettesítse ez az érték: A = π (4/2) 2
  • Osszuk 2 átmérője: d / 2 = 4/2 = 2
  • Eredmény a négyzeten: 2 2 = 4
  • Szorozzuk száma „pi»: A = 4π = 12,56 m 2

Gyakorlat néhány példát. Most, hogy tudod, hogy a formula, próbálja megoldani számos problémát. A több problémát megoldani, annál gyorsabban megtanulják, hogyan kell kezelni őket.

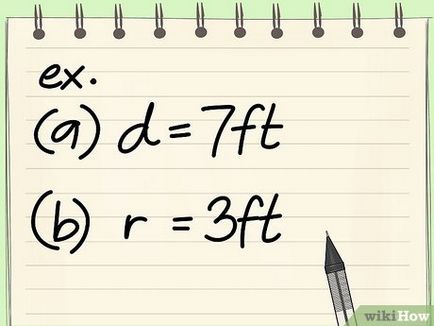
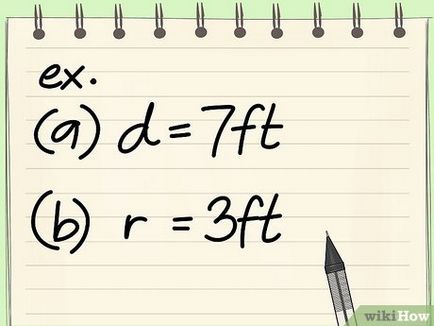
• Keresse meg a terület egy kör átmérője 7 m.
  • A = π (d / 2) 2 = π (7/2) 2 = π (3,5) 2 = 12,25 * π = 38,47 m 2.
• Keresse meg a terület egy kör sugara 3 m.
  • A = πr 2 = π3 2 = 9 * π = 28,26 m 2