Hogyan lehet megoldani polinomok 1
A matematika, a polinom (vagy polinom) - az összege vagy különbsége egytagú. Egytagú közé változók és konstansok, például egytagú 4, -10x és 3x 3. A polinomiális bármelyikéből áll a véges számú egytagú, amelyek nem tartalmaznak negatív kitevőket (x -3), a változók a nevezőben (1 / x) és a változó jelzett négyzetgyök. Megoldani egy polinom, akkor meg kell, hogy megtudja, milyen értékeket „x” polinom nulla.
lépések szerkesztése
1. módszer 5:
Vedd polinom szerkesztése


- Ne feledje, hogy a negatív kifejezés mindig negatív, akkor is, ha a rekord az első ciklus. Nézd meg az előző példában; tag - x 5 negatív volt (mert levonva), így nem volt negatív, ha már felvett első tagja.
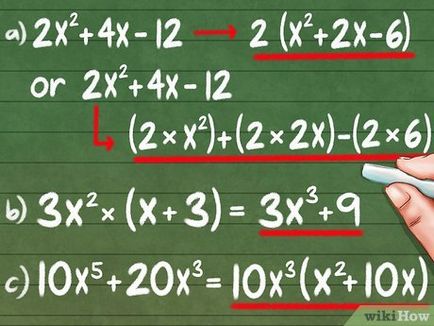
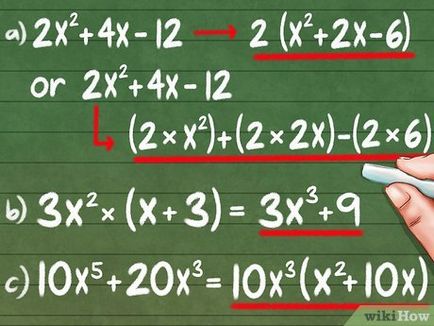
- Annak ellenőrzésére, számítás, szaporodnak mindegyik kifejezés viszont 2. Amennyiben az eredeti polinom: 2x 2 + 4x - 12 = (2 * x 2) + (2 * 2x) - (2 * 6)
- Ez a módszer is alkalmazható a változók, például: 3x 2 * (x + 3) = 3x 3 + 9x 2.
- Mindig vegye ki a zárójelben a legnagyobb szorzó. A polinom 5 10x + 20x 3 A zárójelben lehetséges nem csak azért, hogy 2, de 10x 3. [1]


- Tartsuk szem előtt, hogy a polinomok, kitevője, amely a 4 (x 4), és a fenti, nagyon nehéz megoldani, de lehetséges, hogy egy grafikus számológép.
- Ha intézkedik a polinom csökkenő sorrendben kitevők, akkor rögzítik szabványosított formátumban.


- Egytagú (vagy tag) - egy matematikai kifejezést magában foglaló, állandó vagy változó és állandó és változó. Például, 5, X, 3t, 15Y 3.
- Polinom (vagy polinom) - az összege vagy különbsége egytagú.
- Szorzó - olyan szám, amelyet megszorozva egy másik számot ad a harmadik. Például, a tényezők a 10 2, 5, 1, 10, mivel ezek a számok szorozva egy másik szám lesz 10. multiplikátor és változók, mint a szorzók egytagú 10x 2, 5, 1, 10 és x.
- Képzés - ez a legnagyobb kitevő a változó, amely egy polinom. Például, a polinom x 5 + 3x + 55 egy ötödik fokú polinommal.
- Trinomiális - polinom amely három egytagú, például 2x 2 + x + 12.
- Binomiális (vagy a bab) - olyan polinom, amely két egytagú, például, x + 9. Vegye figyelembe, hogy egyes polinomok bontható két vagy több tényező binomials.
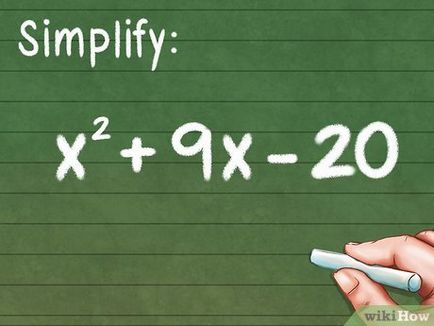
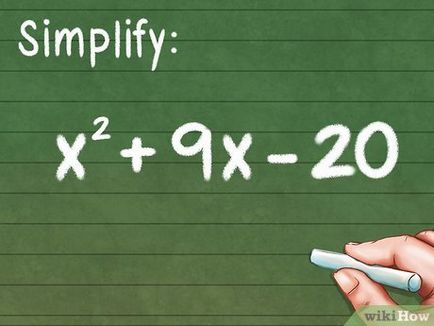
Problémák polinom, amely adni, mint egy trinomiális. Ez a cikk ismerteti csak a másodfokú polinom (az intézkedés a mértéke kisebb, mint 2, például az x 2 3x 2, és így tovább), mert az ilyen trinomiális a leggyakoribb és könnyen megoldani. Trinomiális kell bontani a termék két binomials az első fokú. Vegyünk egy példát: x 2 + 9x - 20.
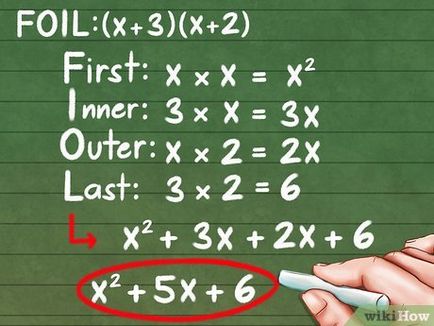
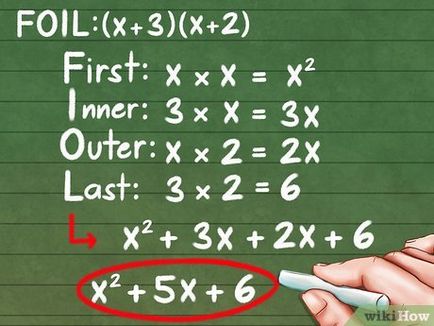
- (X + 3) (x + 2)
- Az első tag. Az első tag az „x”.
- X * x = x 2
- Az első és a második értelemben. Az első tag „X” és a második 2.
- X * 2 = 2x
- A második és az első tag. 3 egy második tag, valamint az első „x.”
- 3 * x = 3x
- A második értelemben. Második feltételek 3. és 2..
- 2 * 3 = 6
- Fold az eredmények, hogy egy többtagú: x 2 + 3x + 2x + 6.
- Fold (vagy kivonás) ezek a tagok, hogy egyszerűsítse polinom (hasonló kifejezések - tagja, amely tartalmaz egy változó egy és ugyanazon exponens): x 2 + 5x + 6
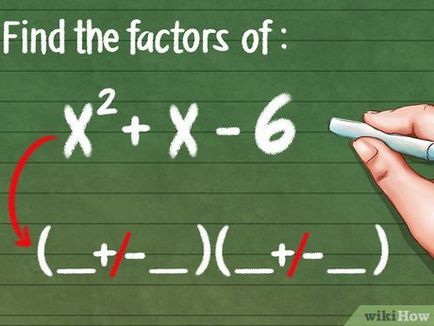
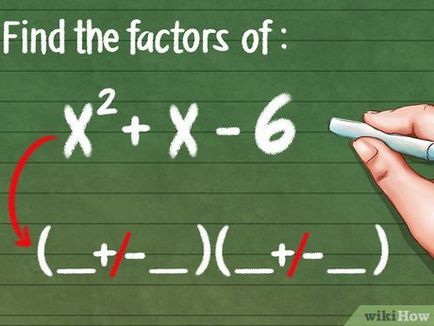
- Az első kifejezés a trinomiális (X 2) az eredménye megszorozzuk az első szempontjából az egyes binomiális.
- A második kifejezés a trinomiális (x) az összege az eredmények a szorzás az első és a második, valamint a második és az első tagjai minden binomiális.
- A harmadik tagja a trinomiális (6) az eredménye megszorozzuk a második szempontjából az egyes binomiális.
- Ha a harmadik negatív trinomiális tagja, a második tagja az egyik binomials negatív.
- Record trinomiális bővítése a termék binomials formájában x 2 + x - 6 = (+/- __ __) (__ + / -__), azaz, hogy megtalálják az egytagú, és helyettesíti őket helyett terek.
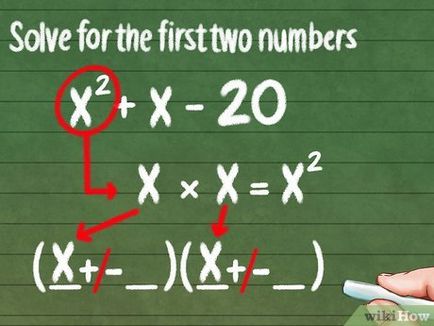
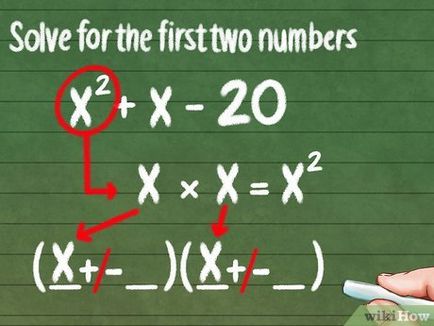
- Talált egytagú helyettesítse első rések az egyes pár zárójelben: (x + / -__) (X +/- __)
- Ne feledje, hogy a tér - a változó vagy állandó, szorozva is.
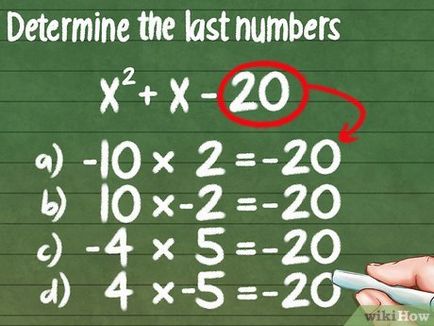
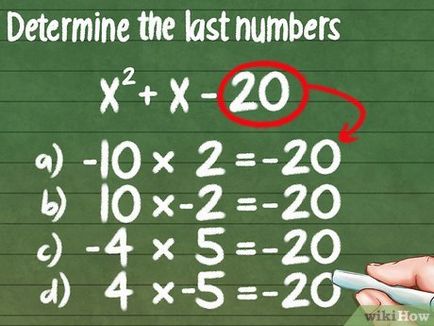
- -10 * 2 = -20
- 10 * -2 = -20
- -4 * 5 = -20
- 4 * -5 = -20
- Megoldása komplex polinomok, akkor tizedesjegy (-3 * 6,6666), de az ilyen polinomok nagyon nehéz megoldani, mivel ez gyakorlatilag lehetetlen alkalmazni az eljárás próbálgatással. Ilyen esetekben használja a grafikus számológép.
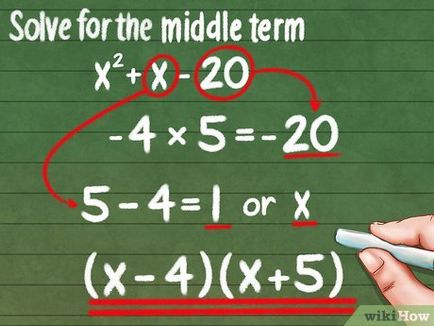
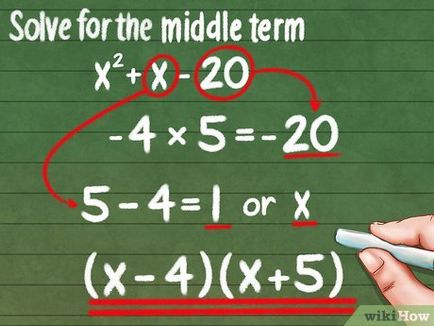
- A pozitív számok azonosítják túlmenően, és negatív - kivonás.
- Megjegyzés. Tekintsük az állandó az első ciklus a háromtagú. Például, ha ebben a példában az első tag trinomiális 3x 2. egy ilyen trinomiális nem bontjuk tényezők (3x-4) (x + 5), mivel ebben az esetben az összege az eredmények darab első és második tagok és az első és második tag nem egyenlő 1: 15 + (-4) = 11. Itt, hogy válasszon egy másik pár szorzók -20.
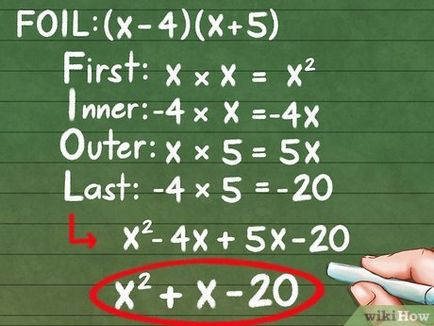
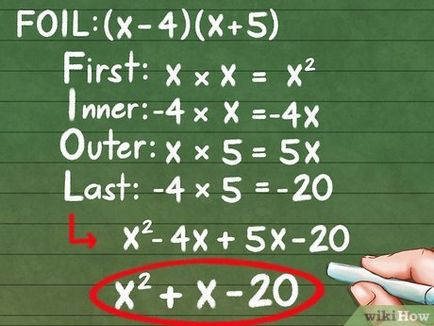
- (4-x) (x + 5)
- Az első tag. X * x = x 2
- Az első és a második értelemben. X * 5 = 5x
- A második és az első tag. * X = -4 -4H
- A második értelemben. -4 * 5 = -20
- Fold az eredmények, hogy egy többtagú: x 2 + 5x - 4x - 20
- Fold, vagy vonjunk hasonló kifejezések: x 2 + x - 20
- Mivel a trinomiális kapott egybeesik a forráskódú megoldás helyes.
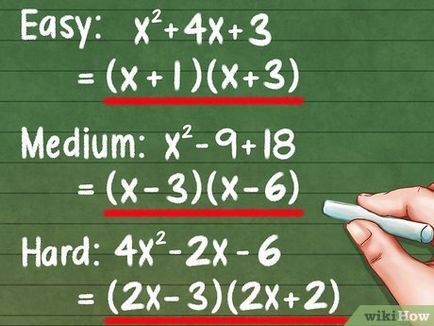
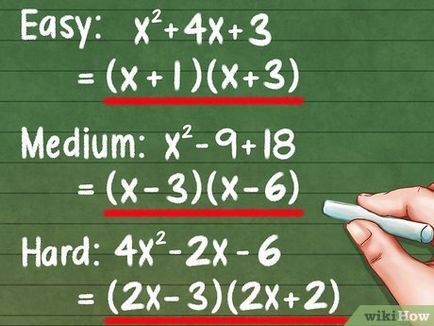
- Egyszerű probléma: x 2 + 4x + 3.
- Válasz: (x + 1) (x + 3)
- A szokásos probléma: X 2 - 9 + 18.
- Válasz: (x-3) (x-6)
- A nehéz feladat: 4x 2 - 2x -6
- Válasz: (2x-3) (2x + 2)


- „Gyökerek” polinom található, ahol ez nulla, azaz a pontok (a koordináta sík), amelyben egy polinomiális függvény grafikon metszi az X tengelyt (vízszintes tengely).


- Egyenlet A: 3x = 0
- B egyenlet: 2x - 4 = 0
- Egyenlet: X + 5 = 0


- Egyenlet A: 3 megsemmisíteni a következő osztály: 3x / 3 = 0/3.
- X = 0
- B egyenlet: 2x - 4 +4 = 0 + 4
- 2x / 2 = 4/2
- X = 2
- C egyenlet: X + 5 - 5 = 0-5
- X = -5
- Meg fogja találni a gyökerei a polinom.
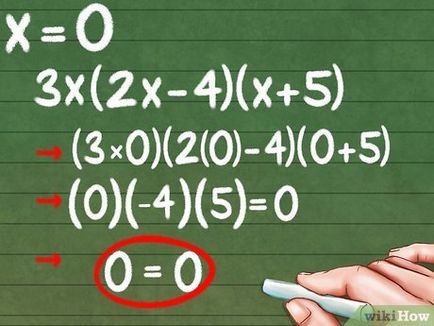
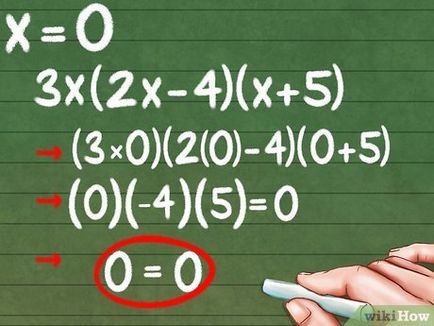
- x = 0: (3 * 0) (2 * 0-4) (0-5) = 0
- (0) (- 4) (- 5) = 0
- 0 = 0
- Helyes. Jelölje be az „x” érték maradt.
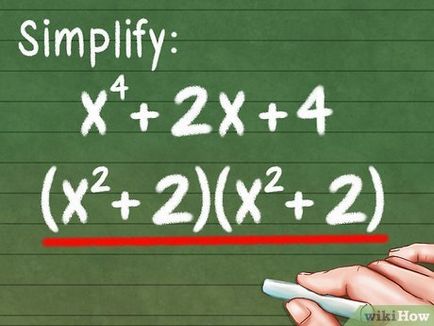
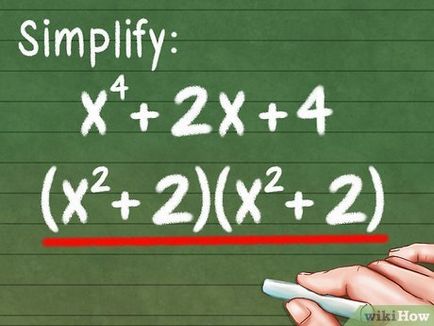
- Mivel a polinom magasabb fokú, például X 4. lehet írva, mint: (X 2) 2. jelentős mértékben egyszerűsíti a megoldást.
- Például X 4 + 2x 2 + 4 = (x 2 + 2) (X 2 + 2)
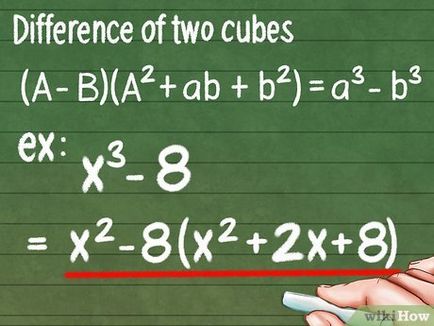
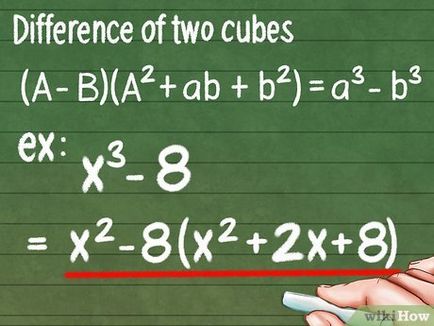
- Ebben a példában, a = x, b = 2 (mert 2 3 = 8). Ezért x 3 - 8 = (x - 2) (X 2 + 2x + 8).
- Ahhoz, hogy megértsük, hogyan ez a képlet származik, keresse fel ezt az oldalt (angol nyelven).


Megtanulják, hogyan kell megoldani egy másodfokú egyenlet. Másodfokú egyenlet - ez a polinom másodfokú, egyenlővé nullára. Másodfokú egyenlet használható megoldására összetett polinomok nélkül grafikus számológép. Segítségével a képlet másodfokú egyenlet megoldása, gyorsan megtalálja a gyökerei a polinom.