egy síkban vektorok

Két vektor párhuzamos síkban helyezkednek nevezzük egy síkban vannak.

Tegyük fel, hogy adottak a három vektor $ \ overrightarrow, \ \ overrightarrow $ és $ \ overrightarrow $. majd

Egy pár vektorok $ \ overrightarrow, \ és \ \ $ overrightarrow, $ \ overrightarrow $ és $ \ overrightarrow $ és $ \ overrightarrow $ és $ \ $ overrightarrow síkban vannak egymással.

Ha két ilyen vektorok, például a $ \ overrightarrow, \ és \ \ $ overrightarrow, egyenesre, akkor a vektorok $ \ overrightarrow, \ \ overrightarrow $ és $ \ $ overrightarrow egy síkban vannak.

Ha $ \ overrightarrow, \ \ overrightarrow $ és $ \ $ overrightarrow fekszenek a síkban vannak egy síkban vannak.

A további megfontolás felidézzük a következő tétel.

Tetszőleges vektor $ \ overrightarrow

$ Bővíthető két nemkollineáris vektorok $ \ overrightarrow \ $ és $ \ $ overrightarrow csak a hőtágulási együtthatók, azaz

Tételek, kapcsolódó koncepció coplanarity három vektorok

Legyen adott egy doboz. Find hármas síkban vektorokat ábrázolja a paralelepipedon az alábbi ábrán.

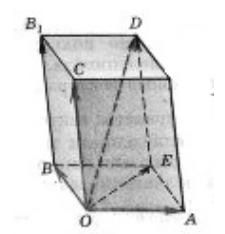
Mivel a vektorok $ \ overrightarrow, \ \ overrightarrow $ és $ \ $ overrightarrow síkban fekszenek $ (BOA) $ akkor ezek a vektorok egy síkban vannak.

Mivel a vektorok $ \ overrightarrow, \ \ overrightarrow $ és $ \ overrightarrow_1> $ síkban fekszenek $ (BOC) $ akkor ezek a vektorok egy síkban vannak.

Mivel a vektorok $ \ overrightarrow, \ \ overrightarrow $ és $ \ $ overrightarrow síkban fekszenek $ (COE) $ akkor ezek a vektorok egy síkban vannak.

Igazoljuk, hogy a vektorok koordinátákkal $ \ left (1 \ 13 \ 2 \ jobbra), \ \ left (3 \ -5 \ 2 \ jobbra) és \ (5, 1,4) $ síkban.

Alkalmazzuk a jele coplanarity három vektorok.

Ezért egy síkban vektorok.