Állapot merőleges vektor

Ebben a cikkben, akkor különös figyelmet fordítanak a feltétele a két, egymásra merőleges vektorok síkban és a háromdimenziós térben, valamint megtalálni a koordinátákat a vektor merőleges egy pár vagy állítsa vektorok. Ez a téma azért fontos, mert van egy jelentős számú problémák (például a kapcsolódó kihívásokat az egyenleteket vonalak és síkok), amelynek megoldása van azon a felismerésen alapul, vektorok merőleges ismert vektorok.

Először fogunk foglalkozni a szükséges és elégséges feltétele két merőleges vektor. Ezután a feltétele merőlegességi megkapjuk vektor megállapítás módszere adott vektor merőleges síkban az űrben. Összefoglalva, nézzük meg egy módja a megállapítás a vektor merőleges mind a két vektor. Figyeljen rá, hogy néhány részletes megoldásokat példa.

Oldalnavigáció.

A szükséges és elégséges feltétele, két merőleges vektor.

Emlékezzünk meghatározását ortogonális vektorok síkban és a háromdimenziós térben.

Két nem nulla vektort nevezzük merőleges. ha a köztük lévő szög egyenlő kilencven fokkal (radiánban).

Milyen gondolatok javaslom ezt a meghatározást, amikor meg kell tudni, hogy két, egymásra merőleges vektor kép, vagy nem?

Ha bizonyos ponton a síkon, hogy késleltesse az egyenlő vektorok megadott vektorokba, majd a szögmérővel tudja mérni a szög közöttük. Ez lehetővé teszi, hogy egy bizonyos fokú pontosság merőlegességi vektorok (ha kapott kilencven fokos szögben mérve). Ebben az esetben, természetesen figyelembe kell venni a pontosság az építési és mérési pontosságot. Egy ilyen eljárás, hogy meghatározzák a szögletességét két vektor kell használni, ha nem tudunk semmit ezek a vektorok, és csak a képet a gépen.

A gyakorlatban gyakran kiderül, hogy a két nem nulla vektor merőlegesség, ha ismert, hogy a koordinátákat a derékszögű koordináta-rendszert a síkban vagy térben. Ebben az esetben, a szükséges és elégséges feltétele két merőleges vektor. Azt állítjuk, hogy a tétel.

A szögletességét két nem nulla vektorok és a szükséges és elégséges az, hogy skalár szorzat értéke nulla, azaz, hogy az egyenlőséget.

Tegyük fel, hogy a vektorok és merőlegesek. Lássuk be az egyenlőséget.

A definíció a skalár szorzata vektorok egyenlő a termék hosszuk a koszinusz az a köztük lévő szög. Mivel a vektorok merőleges, a köztük lévő szög egyenlő kilencven fokkal, ezért, mint szükséges.

Azt viszont, hogy a második rész a bizonyíték.

Most gondolkodunk. Mi bizonyítja, hogy a vektorok és merőlegesek egymásra.

Mivel a vektorok és nem nulla, akkor következik az, hogy. Így a koszinusza közötti szög vektorok egyenlő nullával, és ebből következően, a szög egyenlő, jelezve, hogy a vektorok és merőlegességi.

Így egy szükséges és elégséges feltétele két merőleges vektorok bizonyult.

Mivel a feltétel úgy néz szögletességét két vektor komponens formájában?

A skaláris szorzat a koordinátákat megmutattuk, hogy két vektor megadott koordináták és a gép közötti egyenlőség, valamint a két vektor a térben. Így a szükséges és elégséges feltétele merőlegességének a két vektor koordinátái egy repülőgépen, és egy háromdimenziós térben.

Tekintsük a kérelem e feltételek a gyakorlatban ez a megoldás elemezni néhány példát.

hogy a vektorok merőleges.

Azzal a feltétellel, merőleges vektorok van. Tegyük fel, majd jön. Tehát a vektor - az egyik a vektorokat, amelyek merőlegesek a vektorba.

.

Hasonlóan keresett vektor merőleges az adott vektor háromdimenziós térben.

A vektor van egy végtelen ortogonális vektorok. Megmutatjuk ezt. Hagyja, hogy a vektor fekszik a vonal egy. Jelölje egy tetszőleges merőleges síkban egy egyenes vonal egy. Ezután minden nem nulla vektor tartozó merőleges síkban a vektor.

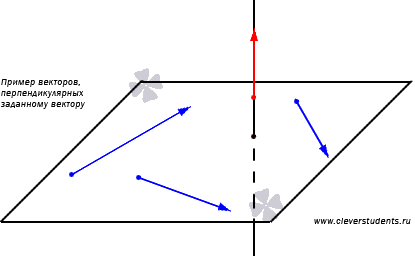
Megmutatjuk, hogyan kell használni a feltételek merőlegességi vektorok koordinátái egy vektor merőleges egy adott, nem-nulla vektor.

Hagyja, hogy a vektor koordinátái és. Megtalálni őket.

A feltétel a két merőleges vektor az egyenlőség. Mivel a vektor nem nulla, akkor legalább az egyik a koordinátái nullától eltérő. Legyen (vagy tudod venni). Akkor lehet osztani a koordináta mindkét fél, ugyanabban az időben beszerezni. Így adva a koordinátákat és önkényes értékek, legalább az egyik, amely nem nulla, és kiszámítása a képlet, kapunk egy vektor merőleges, az adott vektort.

Nézzük a következő példát.

Keresse meg a koordinátáit egy vektor merőleges vektor.