Alapvető (core) és a szabad (nem mag) változók

A téma „Kronecker-Capelli tétel”, azt állította, hogy ha a rangot a mátrix rendszer bővítését $ \ widetilde $ rang és mátrix rendszer $ A $ egyenlő, akkor az adott rendszer lineáris algebrai egyenletek (SLAE) kompatibilis, azaz a Ez egy megoldás. A kérdés a megoldások száma lehetővé tette a vizsgálat Kronecker. Elmondása szerint, ha $ \ megcsörrent A = \ csengetett \ widetilde = n $ ($ n $ - szám ismeretlen), hogy Slough egyedülálló megoldás. Ha $ \ megcsörrent A = \ csengetett \ widetilde

Különösen érdekes a helyzet a $ \ csengett A = \ csengetett \ widetilde

Mit jelent a „rangot egyenlő $ r $”? Ez azt jelenti, hogy van legalább egy kisebb $ r $ edrendű, ami nem nulla. Emlékszem, hogy egy kiskorú az úgynevezett alap. Alapján kiskorúak is több. Így minden kiskorú, akinek érdekében áll a fenti $ r $, nullával egyenlő, vagy nem létezik.

Ha az együtthatók a változók $ r $ együtt SLAE alapján kisebb mátrix rendszer $ A $, akkor ezeket a változókat $ r $ úgynevezett alap- vagy alapvető. A fennmaradó $ n-R $ változók úgynevezett szabad vagy nem-core.

$ R $ Select alapváltozó általában lehet a legkülönfélébb módokon. A példákban azt fogja mutatni a leggyakrabban használt módszer a választás.

Megoldás Slough. amelyben az összes szabad változók értéke nulla, az úgynevezett bázis.

Az összes alábbi példákban a mátrix rendszer jelöli $ A $ és a kiegészített mátrix rendszer - a levél $ \ widetilde $.

Problémák a lineáris rendszerek $ \ left \<\begin & 3x_1-6x_2+9x_3+13x_4=9\\ & -x_1+2x_2+x_3+x_4=-11;\\ & x_1-2x_2+2x_3+3x_4=5. \end \right.$. Если система является неопределённой, указать базисное решение.

Tehát van lineáris rendszerek amely 3 egyenletek és 4 változó: $ x_1 $, $ x_2 $, $ x_3 $, $ x_4 $. Mivel a változók száma nagyobb, mint ahány egyenlet, egy ilyen rendszer nem rendelkezik egyedi megoldás (egy kicsit később azt szigorúan bizonyítani a javaslat alapján a Kronecker-Capelli). Slough megoldást találni Gauss:

$$ \ left (\ begin 3 -6 9 13 9 \\ -1 2 1 1 -11 \\ 1 -2 2 3 5 \ end \ right) \ rightarrow \ left | \ begin \ Szöveg \\ \ Szöveg \\ \ Szöveg \ end \ right | \ Rightarrow \\ \ rightarrow \ left (\ begin 1 -2 2 3 5 \\ -1 2 1 1 -11 \\ 3 -6 9 13 9 \ end \ right) \ kezdődik \ fantom \\ II + I \\ III-3 \ cdot I \ végén \ rightarrow \ left (\ kezdődik 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 3 4 -6 \ end \ right) \ kezdődik \ fantom \\ \ fantom \\ III-II \ end \ rightarrow \\ \ rightarrow \ left (\ kezdődik 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ end \ right) $$

Átadtuk előremenetben a Gauss módszer, így a kibővített mátrixát a rendszer lépcső formában. Ahhoz, hogy a bal oldalon a funkciók a mátrix elemei a transzformált rendszer, mi is vezetett Echelon formában. Hadd emlékeztessem önöket, hogy ha kap egy bizonyos mátrix Echelon formában, majd a rangsorban egyenlő száma nulla sorok.

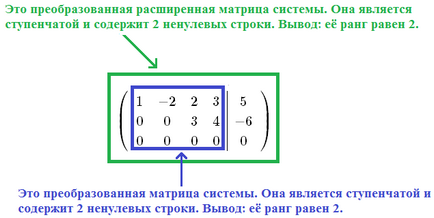
És a rendszer mátrix és a kiterjesztett mátrix rendszer után egyenértékű transzformációk csökken lépcső formájában; Ezek két nullától vonalon. Következtetés: $ \ megcsörrent A = \ csengetett \ widetilde = 2 $.

Így, mivel SLAE tartalmaz négy változó (jelöljük száma $ N $, azaz $ n = 4 $). Továbbá, a rendszer rangsorolja a rendszer, és a kiegészített mátrix a mátrix egyenlők egymással és egyenlők az számát $ r = $ 2. Mivel a $ r

Találunk ezeket a megoldásokat. Elsőként válassza az alapvető változókat. Számuk egyenlőnek kell lennie a $ r $, azaz A mi esetünkben két alapvető változókat. Milyen változók (mert van nekik 4 db), hogy elfogadja az alapját? Jellemzően az alapvető változók veszik azokat a változókat, amelyek székhelye az első helyen a nulla sorban a transzformált mátrix rendszer, azaz a a „lépés”. Mi ez a „lépés” az alábbiakban mutatjuk be:

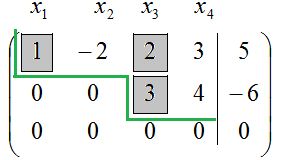
A „lépések” az oszlopok száma №1 és №3. Az első oszlop megfelel a változó $ x_1 $, és a harmadik oszlop megfelel a változó $ x_3 $. Hogy a változók $ x_1 $ és $ $ x_3 veszi alapul.

Miért nem tudjuk elfogadni a változók $ x_1 $ és $ $ x_3 alapul? A kérdés megválaszolásához Idézzük hogy a rangot a rendszer száma $ r = 2 $. Azt mondja, hogy az összes kiskorú e mátrix. érdekében, nagyobb, mint 2, vagy egyenlő nullával, vagy nem létezik. Zéró kiskorúak kiskorúak körében már csak másodrendű. Úgy döntünk, bármely nem nulla kisebb másodrendű. Mi lehet választani, mint az eredeti mátrix rendszer $ A $, azaz A mátrixban $ \ left (\ begin 3 -6 9 13 \\ -1 2 1 1 \\ 1 -2 2 3 \ end \ right) $, és a transzformált rendszer mátrix, azaz a A $ \ left (\ begin 1 -2 2 3 \\ 0 0 3 4 \\ 0 0 0 0 \ end \ right) $. Mivel a transzformációs mátrix több nulla a rendszer, akkor működni fog vele.

Úgyhogy válaszd a másodrendű kisebb elemeket, amelyek a kereszteződésekben a vonalak №1 és №2, és oszlopok №1 és №2:

Következtetés: A kijelölt személy Minor másodrendű nem alapvető, mert nulla. Mivel az elemek ezt az apró vesszük az oszlopról №1 (ez felel meg a változó $ x_1 $) és az oszlop №2 (ez felel meg a változó $ x_2 $), akkor a két változó $ x_1 $ és $ $ x_2 nem lehet alapvető változókat.

Készíts egy második kísérlet, hogy egy kisebb másodrendű elemek fekszenek a kereszteződésekben a vonalak №1, №2 és oszlopok №2 és №4:

Következtetés: A kijelölt személy kiskorú másodrendű alapján, mivel nem nulla. Mivel az elemek ezt az apró vesszük az oszlopról №2 (ez felel meg a változó $ x_2 $) és az oszlop №4 (ez felel meg a változó $ x_4 $), egy pár változó x_2 $ $ és $ $ X_4 lehet alapul venni.

Csináljunk egy harmadik kísérlet, és megállapította, az érték a kisebb, az elemek, amelyek kereszteződésénél található a sorok №1, №2 és oszlopok №1 és №3:

Következtetés: A kijelölt személy kiskorú másodrendű alapján, mivel nem nulla. Mivel az elemek ezt az apró vesszük az oszlopról №1 (ez felel meg a változó $ x_1 $) és az oszlop №3 (ez felel meg a változó $ x_3 $), egy pár változó $ x_1 $ és $ $ x_3 lehet alapul venni.

Mint látható, a kiválasztás alapváltozó nem egyértelmű. Valójában a több választási nem magasabb, mint azon helyek számát a $ n $ elemek $ R $, azaz nem több, mint $ C $ _ ^.

Ebben a példában a baisnyh fogadták változók $ x_1 $ és $ x_3 $ - pusztán kényelmi okokból a további megoldásokat. Mi ez a kényelem, látni fogjuk, egy kicsit később.

Alapvető változókat úgy választjuk: ez $ x_1 $ és $ x_3 $. A fennmaradó $ n-r = 2 $ változók (azaz a $ x_2 $ és $ x_4 $) szabadon. Meg kell, hogy kifejezze a alapváltozó keresztül ingyenes.

Inkább dolgozni a rendszer mátrix formában. Kezdeni tisztít kapott mátrix $ \ left (\ begin 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ end \ right) $ a nulla vonal:

$$ \ left (\ begin 1 -2 2 3 5 \\ 0 0 3 4 -6 \ end \ right) $$

Szabad változók, azaz a $ X_2 $ és $ x_4 $, a megfelelő oszlop №2 és №4. Gyors előre ezeket az oszlopokat át a vonalon. Bejelentkezés minden elemét hordozza az oszlop fogja változtatni az ellenkezője:

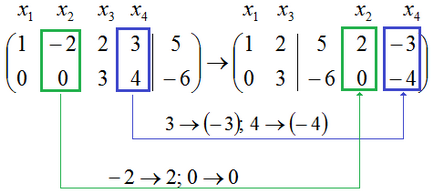
Miért kapok a jeleket? Mindez azt átadó oszlopokat? Megjelenítése \ elrejtése

Térjünk át a kiterjesztett rendszer mátrix, amely után az átalakítás az űrlap $ \ left (\ begin 1 -2 2 3 5 \\ 0 0 3 4 -6 \ end \ right) $. Térjünk át a mátrix egyenletek. Az első sor megfelel az egyenlet $ x_1-2x_2 + 2x_3 + 3x_4 = $ 5, és a második vonal megfelel az egyenlet $ 3x_3 + 4x_4 = -6 $. Most át a szabad változók x_2 $ $ és $ $ X_4 a jobb oldalán egyenletek. Természetesen, amikor megyünk a kifejezést $ 4x_4 $ a jobb oldalon az egyenlet, a jel meg fogja változtatni az ellenkező, és a jobb oldalon lesz $ -4x_4 $.

\ begin x_1 + 2x_3 = 5 + 2x_2-3x_4; \\ 3x_3 = -6-4x_4. \ end

Ha újra felvenni a kapott rendszer a mátrix formájában, megkapjuk a mátrix oszlopai költözött át a vonalon.

És most továbbra is foglalkozzon a szokásos módon Gauss. Célunk: hogy a mátrix az a készülék szolgáltatásai. Először, ossza el a második sor 3, majd továbbra is átalakítja vissza helyettesítő módszer:

$$ \ left (\ begin 1 2 5 2 -3 \\ 0 3 -6 0 -4 \ end \ right) \ kezdődik \ fantom \\ II: 3 \ end \ rightarrow \ left (\ kezdődik 1 2 5 2 -3 \\ 0 1 -2 0 -4/3 \ end \ right) \ begin I-2 \ cdot II \\ \ fantom \ end \ rightarrow \\ \ rightarrow \ left (\ begin 1 0 9 2 1/3 \\ 0 1 -2 0 -4/3 \ end \ right). $$

A Matrix jellemzői, hogy legyen egy egységes, befejezett Gauss. Az általános megoldás, már csak azt kell írni. Ha arra gondolunk, hogy a negyedik oszlop megfelel a változó $ x_2 $, az ötödik oszlop - változó $ $ X_4, kapjuk:

Megszereztük az általános megoldás adott SLAE. Ahhoz, hogy megtalálja a lúgos oldatot, szükség van az összes szabad változók nullának. Ie feltételezve $ x_2 = 0 $ és $ x_4 = 0 $, van:

Megoldás $ x_1 = 9 $, $ x_2 = 0 $, $ x_3 = -2 $, $ x_4 = 0, és $ jelentése az alap megoldás erre SLAE. Elvileg a beállítás szabad változók más értékek, akkor kap más különös megoldást a rendszer. Ilyen saját végtelen számú megoldást. Például, figyelembe $ x_2 = -4 $ és $ x_4 = 1 $, megkapjuk egy adott megoldás: $ \ left \ x_1 = \ frac; \\ x_2 = -4; \\ x_3 = - \ frac; \\ x_4 = 1. \ End \ right. $. Basic megoldás, amit találtam korábban - csak egy a végtelen számú egyedi megoldásokat adott Slough.

Ha szeretné, a kapott oldatot lehet ellenőrizni. Például, hogy ebben az esetben $ x_1 = 9 + 2x_2- \ fracx_4 $ és $ x_3 = -2- \ fracx_4 $ a bal oldalon az első egyenlet, kapjuk:

$$ 3x_1-6x_2 + 9x_3 + 13x_4 = 3 \ cdot \ left (9 + 2x_2- \ fracx_4 \ right) -6x_2 + 9 \ cdot \ left (-2- \ fracx_4 \ jobb) + 13x_4 = 9. $$

Ellenőrzés első egyenletből sikertelen; ugyanúgy ellenőrizni tudja a második és a harmadik egyenlet.

Válasz. Az általános megoldás: $ \ left \ x_1 = 9 + 2x_2- \ fracx_4; \\ x_2 \ K; \\ x_3 = -2- \ fracx_4; \\ . X_4 \ R. \ end \ right $, az alapvető megoldás: $ \ left \ x_1 = 9; \\ x_2 = 0; \\ x_3 = -2; \\ x_4 = 0. \ End \ right. $.

Problémák a lineáris rendszerek $ \ left \ x_1-2x_2 + 4x_3 + 2x_5 = 0; \\ 4x_1-11x_2 + 21x_3-2x_4 + 3x_5 = -1; \\ -3x_1 + 5x_2-13x_3-4x_4 + x_5 = -2. \ End \ right. $. Ha a rendszer bizonytalan, adja meg az alapvető megoldás.

Egy hasonló példa már megoldódott a tárgy „módszer Kramer” (példa №4). Változók $ X_4 $ és $ x_5 $ átkerült a jobb oldalán, majd a használt szabványos működési módja Kramer. Ez a módszer azonban nem garantálja megoldásokat eredményeket elérni. Például, visszük néhány változót a jobb oldali, és a fennmaradó meghatározó nullával egyenlő, - akkor mi lesz? Brute force megoldani. ) Ezért sokkal kényelmesebb használni az átalakulás a Gauss módszer. mint az előző példában.

$$ \ left (\ begin 1 -2 4 0 2 0 \\ 4 -11 21 -2 3 -1 \\ -3 5 -13 -4 1 -2 \ end \ right) \ kezdődik \ fantom \\ II-4 \ cdot I \\ III + 3 \ cdot I \ végén \ rightarrow \ left (\ kezdődik 1 -2 4 0 2 0 \\ 0 -3 5 -2 -5 -1 \\ 0 -1 -1 -4 7 -2 \ end \ right) \ rightarrow \\ \ rightarrow \ left | \ begin \ Szöveg \\ \ Szöveg \\ \ Szöveg \ end \ right | \ rightarrow \ left (\ begin 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ -3 5 -2 -5 -1 \ end \ right) \ kezdődik \ fantom \\ \ fantom \\ III-3 \ cdot I \ végén \ rightarrow \\ \ rightarrow \ left (\ kezdődik 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ 0 8 10 -26 5 \ end \ right). $$

A mátrix rendszer, és a speciális mátrix a rendszer csökken egy trapéz alakú. Fokozatú ilyen mátrixok egyenlők egymással és egyenlők az 3-as szám, azaz a $ \ Rang A = \ csengetett \ widetilde = 3 $. Mivel a soraiban egyenlő vagy kisebb, mint a változók száma szerint a vizsgálat a Kronecker-Capelli ez a rendszer végtelen számú megoldást.

Az ismeretlenek száma $ n = 5 $, soraiban egyaránt mátrixok $ r = 3 $, így meg kell választani három alapvető változók és a $ n-r = $ 2 szabad változók. Ugyanazokat a „lépés” módszer, mint az előző példában, úgy döntünk, mint az alap változó $ x_1 $, $ x_2 $, $ x_3 $, valamint a szabad változók - $ x_4 $ és $ x_5 $.

Oszlopok №4 és №5, amelyek megfelelnek a szabad változók, gyors előre a sorban. Ezután ossza el a harmadik 8 vezetéken és kiterjesztése oldatot Gauss módszer:

$$ \ left (\ begin 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 8 5 -10 26 \ end \ right) \ kezdődik \ fantom \\ \ fantom \\ III: 8 \ end \ rightarrow \ left (\ kezdődik 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 1 5/8 -5/4 13/4 \ end \ right) \ kezdődik I-4 \ cdot III \\ II + III \\ \ fantom \ end \ rightarrow \\ \ left (\ kezdődik 1 -2 0 -5/2 5 -15 \\ 0 -1 0 -11/8 11/4 -15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ right) \ kezdődik \ fantom \\ II \ cdot (-1) \\ \ fantom \ end \ rightarrow \ left (\ kezdődik 1 -2 0 -5/2 5 -15 \\ 0 1 0 08/11 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ right) \ kezdődik I + 2 \ cdot II \\ \ fantom \\ \ fantom \ end \ rightarrow \\ \ rightarrow \ left (\ kezdődik 1 0 0 1/4 -1/2 -15/2 \\ 0 1 0 08/11 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ right) $$

Az utolsó a mátrix egy közös megoldást egy adott lineáris rendszer: $ \ left \ x_1 = \ Frac \ fracx_4- \ fracx_5; \\ x_2 = \ Frac \ fracx_4 + \ fracx_5; \\ x_3 = \ Frac \ fracx_4 + \ fracx_5; \\ x_4 \ K; \\ x_5 \ R. \ end \ right. $. Lúgos oldatot kapunk, ha a szabad változók nullának, azaz $ X_4 = 0 $, $ x_5 = 0 $:

Folytatása ez a téma, úgy a második rész. Nézzük meg, ahol még két példát találni a közös megoldást.