A terület a palástfelület egy csonka - általános képletű Például, számológép

Csonka gúla - poliéder, ami úgy alakul ki az alapja a piramis rész, és azzal párhuzamosan. Elmondhatjuk, hogy a csonka gúla - a piramis tetején. Ez a minta számos egyedi tulajdonságokkal rendelkezik:

• A oldalfelületei A piramis a trapéz;
• A oldalélei egyenlő hosszúságú, és a helyes csonkagúla vannak döntve, hogy a bázis ugyanolyan szögben;
• Bázisok hasonlóak poligonok;
• A csonka egyenes gúla arcok azonosak egyenlő szárú trapéz területének amely egyenlő. Ők is hajlik arra, hogy a talaj ugyanolyan szögben.

Képlet területe a palástfelület egy csonka gúla képviseli négyzetösszege az oldalán:

Mivel az oldalán a piramisok csonka trapéz, hogy ki lehessen számítani a szükséges paramétereket kell használni a képlet trapéz területe. Ahhoz, hogy megfelelően csonka gúla lehet alkalmazni egy másik képlet a környéken. Mivel annak minden oldala nézzen, és a bázis szögek egyenlőek, lehetőség van alkalmazni a kerülete a bázis és apofemu és megjelenítési területen keresztül a sarokban a tövénél.

Ha a feltételeket a megfelelő csonka piramis apothem (H oldal), és a hossza az oldalán a bázis, ez lehet számítani a területen keresztül poluproizvedenie összege kerülete a bázisok és apothem:

Nézzünk egy példát terület kiszámításával az oldalsó felületén csonka gúla.
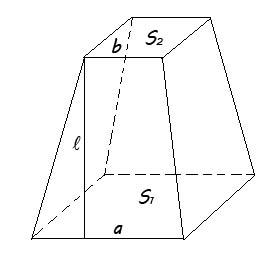
Dana ötszögű piramis. Apothem l = 5 cm, hossz alapján egy nagy arcok egy = 6 cm, és az arc a kisebb bázis b = 4 cm. Számítsuk ki a négyzet alakú csonka gúla.

Kezdeni, meg a kerülete a bázisok. Mivel adott egy ötszögű piramis, megértjük, hogy a bázisok ötszög. Tehát az okok ez ugyanaz a szám öt oldala van. Találunk a kerülete a nagyobbik alapja:

Ugyanígy találunk a kerülete kisebb bázis:

Most tudjuk számítani a területet rendszeresen csonka gúla. Helyettesítse az adatokat a képlet:

Így számított területének rendszeres csonka gúla keresztül kerülete apofemu.

Egy másik módszer kiszámítására a terület az oldalsó felületének egy szabályos piramis, a képlet a szögek a tövénél terület és a legtöbb ilyen bázisok.

Nézzünk egy példát számítás. Ne feledje, hogy ez a képlet csak a helyes csonka gúla.

Legyen egy szabályos négyszögletes piramis. Egy arc az alacsonyabb bázis a = 6 cm, és a felső határ b = 4 cm. Diéderes szög tövénél β = 60 °. Keresse meg a megfelelő területet az oldalsó felület csonka gúla.

Kezdeni számítani a területen bázisok. Mivel a jobb piramis, a bázisok az összes arcot egyenlő. Tekintettel arra, hogy az alap négyszög, megértjük, hogy akkor kell számítani a területen egy négyzet. Ez a termék a szélessége a hosszúság, de ezek az értékek azonosak a téren. További helyigény:


Most használd a kapott értékeket kiszámításához az oldalsó felülete.

Ismerve néhány egyszerű képletek, akkor könnyen kiszámítható a területet a trapéz oldalán csonka gúla keresztül különböző értékeket.