A normális eloszlás (Gauss-féle eloszlás)
A berendezés a matematikai statisztika meglehetősen jól kidolgozott kapcsolatban a feltétellel, ha az eloszlás valószínűségi változó engedelmeskedik normális eloszlás (Gauss-törvény).
Tanulmányok gépészet úgy találta, hogy a legtöbb jellemzőit a technológiai folyamatok is vonatkozik ez a törvény.
Normális eloszlás döntő szerepet játszik minden területén a mérnöki és a technológia, és különleges helyet foglal el a többi törvényei forgalmazás.
Normális eloszlás valószínűségi változó felmerül azokban az esetekben, amikor a vizsgálat eredménye következtében számos tényező, amelyek között nem domináns, és a hangerő megfigyelés elég nagy. Sok folyamatos felügyelet növekvő vizsgált anyag mennyiségének hajlamos a normális eloszlás.
Egy véletlen változó normális eloszlású, ha az egyenlet sűrűségfüggvény van:
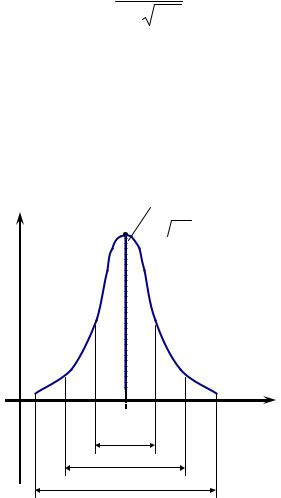
Az elméleti görbéje a törvény a normál eloszlás harang alakú, szimmetrikus a merőleges az X-tengelyen átmenő ponton az x-tengely az Y koordinátája a. Ez eléri maximális ezen a ponton (0 1 σ 2 π) aszimptotikusan nullához közelít
Az elvárás: M (Y) = Y 0. Diszperziós: D (Y) = σ 0 2.
A görbe alatti terület határolt intervallumban Y 1 ≤Y ≤Y 2. 0 megfelel a valószínűsége, hogy a kísérleti eredmények fog esni a nyílásba. Belül ± 3σ 0 y 0 99,73% a görbe alatti terület.
Ezért a gyakorlatban a normális eloszlást használjuk a „három szigma szabály”. A törvény a normális eloszlás alapján a „hármas szabály szigma” p szórás területén a valószínűségi változó:
p = (Y O + 3 σ o) - (Y o - 3 σ o) = 6 σ o.
Annak a ténynek köszönhetően, hogy a becslés σ 0 és x 0 segítségével a jellemzői a minta S és X, gyakorlati szórt mező határozza meg a képlet:
ahol l - együtthatót táblázat értéket vett egy adott mintaméret α = 0,95 (ahol L jelentése számítva a feltétellel, hogy a szám a véletlen változók, amelyek a gyakorlati szórt mező 99,73%).
Példák a normális eloszlás:
- az elosztó a hiba mérőműszerek;
- mérési jellemző paraméter az ugyanabból a tételből termékek;
- pozicionálási hibáját CNC szerszámgépek, robotok, stb