A hallgatók felkészítése a vizsgát, és OGE (DPA), a képzési központ felbontású (kézikönyv a matematika -

átalakítani sík

Definíció 1. Az átalakulás a sík nevezzük szabályt. amelynek minden pontja a sík tartozik egy pont a síkban.

A meghatározás 1 azt jelenti, hogy ha F - transzformáció a sík α. és M - tetszőleges pont a sík. az F (M) is egy pont a sík α.

2. meghatározása Point F (M) az úgynevezett image M pont, amikor konvertáló M pont F. prototípus úgynevezett F (M) ponton konvertáló F.

Meghatározása hasonlóan inverz képeket bármely darabok az átalakulás síkon F.

3. meghatározása Transform sík nevű bijektív transzformáció síkon is. ha a különböző pontjain különböző képeket. és mindegyik pont a fordítottja képsík.

Más szóval, ha egy-egy átalakulás a sík különböző pontjai a sík mozgó különböző részein ugyanabban a síkban, és minden pontján a repülőgép halad bizonyos ponton ez a sík.

MEGHATÁROZÁSA 4. A terméket (összetétel) a két transzformáció az úgynevezett transzformáció, amelyet úgy kapunk, hogy egymás után végrehajtja ezeket transzformációk.

Így, ha az F és G - két konverziót, a termék Ezen transzformációk lesz átalakítása H, A jelentése egy tetszőleges pont egy síkban kell mutatnia A „ez a sík, képlet határozza meg:

A síkokban

DEFINÍCIÓ 5. Mozgás síkon úgynevezett transzformációs síkban, ahol a távolság két pont a síkon egyenlő a távolságot a képeket.

Az alábbi transzformációk síkban mozgások:

1. Párhuzamos transzfer (shift) egy előre meghatározott vektor

Ezzel párhuzamosan szállítási síkban egy előre meghatározott vektor (1. ábra) A sík egy tetszőleges pontjának bemegy egy pont A „síkban a egyenlőség

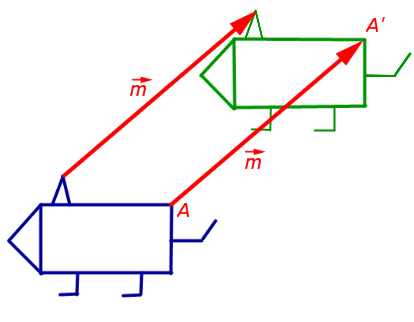
Megjegyzés. Mozgás, amelyben minden pont a síkban marad a helyén, az úgynevezett identitás átalakulása. A személyazonosító transzformációs lehet tekinteni, mint egy párhuzamos fordítást egy vektor nullával egyenlő.

2. forgatás a specifikus pont az úgynevezett forgási középpont előre meghatározott szögben

Forgatásával a gép körül az O pont szögben φ (ábra. 2) egy tetszőleges pontjának a síkban halad egy pont A „síkban, hogy a egyenlőségek

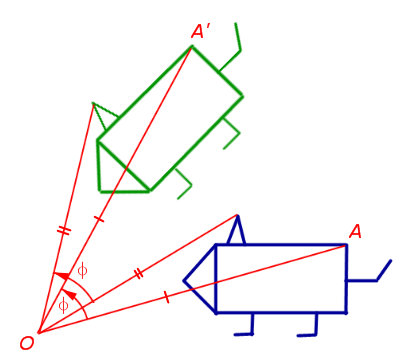
3. A központi szimmetria (szimmetria egy előre meghatározott ponton úgynevezett központjában szimmetria)

A központi szimmetriasíkkal képest az O pont tetszőleges pontja Egy a síkon halad egy pont A „síkban van, mint a középpontját a szegmens AA” ez az a pont, O - előre meghatározott szimmetria központja (3. ábra).

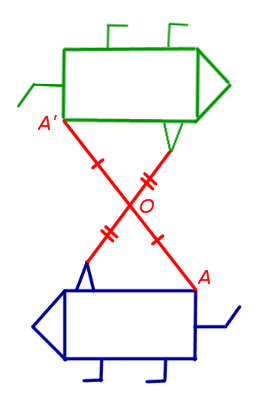
4. tengelyszimmetrikus (szimmetria az adott sorban, az úgynevezett szimmetriatengelye)

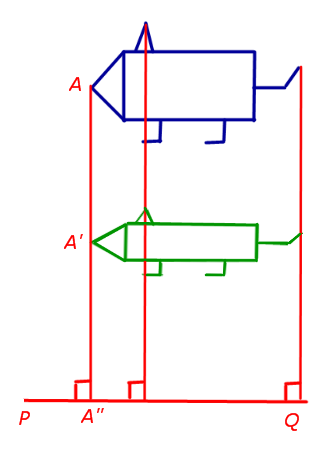
Amikor tengelyszimmetrikus képest egy egyenes vonal PQ (szimmetriatengelye) egy tetszőleges pontjának a síkban halad egy pont A „síkban, hogy egyrészt, a AA” vonal merőleges a PQ egyenes. és másodszor, a metszéspont az AA „és PQ az a felezőpontja AA”

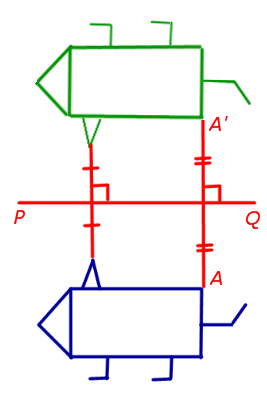
5. Csúszó szimmetria (összetétele tengelyszimmetrikus képest az adott sorban és párhuzamos transzferázok egy előre meghatározott nemnulla vektor párhuzamos e egyenes vonal)

Ha a vonal PQ - szimmetria tengelye, és a párhuzamos fordítás vektort adott egy párhuzamos vonal PQ. mozog a szimmetria eredményt hagyományos módon lehet az alábbi képlettel ábrázolható, ahogy az 5. ábrán látható.

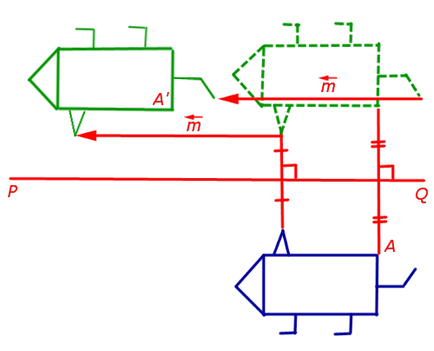
Motion sík orientáció megőrzése. Motion sík változó irányú. tétel Sala

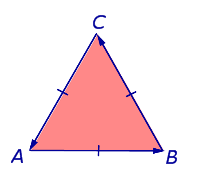
Tekintsünk egy tetszőleges síkban, egyenlő oldalú háromszög, és a betűk jelölik a csúcsokat A, B és C, hogy megy végig az oldalán a háromszög irányába

háromszög vannak elrendezve a bal oldalon (ábra6). Ezzel a jelöléssel a csúcsok egy háromszög túra kerül sor az óramutató járásával ellentétes.

Tegyük fel, hogy bizonyos mozgás F veszi az ABC háromszög a A'B'C háromszög”, amelyet

Mivel minden mozgás a síkban tartja a pontok közötti távolság, a háromszög A'B'C „is szabályos, de a következő két esetben.

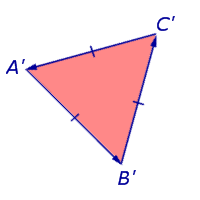
Az első esetben, a bypass oldalán a háromszög A'B'C „abba az irányba

Triangle A'B'C „található a bal oldalon. és bypass végezzük óramutató járásával ellentétes irányban (7. ábra).

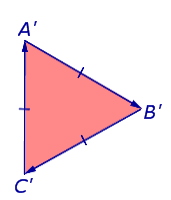
A második esetben, egy áramköri oldalai mentén a háromszög A'B'C „irányban

Triangle A'B'C „található a jobb oldalon. és bypass végezzük az óramutató járásával megegyező irányban (8. ábra).

Definíció 6. Ha az első eset valósul meg, amikor a mozgó F, akkor ez a mozgás a mozgás, amely megőrzi a sík orientáció (a mozgás az 1. típusú, megfelelő mozgás). Ha az F-motion hajtjuk végre a második esetben egy ilyen mozgalom az úgynevezett motion, tájolásának megváltoztatása (mozgás a 2. típusú, nem megfelelő mozgás).

Osztályozási rendszere mozgások a sík meghozta a következő tétel Sala.

Chasles tétel. Bármely mozgás síkban orientáció megőrzése, vagy párhuzamosan elmozdítható. vagy fordult. Bármely mozgás síkban változó orientáció, jelentése vagy axiális szimmetria. vagy csúsztatva tükrözés.

Affin transzformáció sík

7. meghatározása affin transzformáció sík az úgynevezett egy-az-egy transzformációs síkban magát, ahol bármely közvetlen módon a sík egy egyenes vonal.

Mivel minden egyes mozgás síkjában hordoz egyenes sorokat egyenes vonalak, minden mozdulat egy affin transzformáció.

Azonban affin transzformációk nem korlátozódnak a síkokban. A következő átalakításokat is affin transzformációk síkban:

1. Compression (nyújtás), hogy a vonal egy előre meghatározott tömörítési arány (expanziós)

A sűrítés alatt (bővítés) a sík egyenes vonalú PQ adja meg a tömörítési arány k (ábra9) A sík egy tetszőleges pontjának bemegy egy pont „síkon, hogy a következő feltételek teljesülnek:

• Közvetlen AA „merőleges a PQ egyenes;
• Ha betűvel jelölt A „metszéspontját az AA„és PQ. lesz egyenlőség

| A'a "| = | k | | AA" | ;

ha k> 0. Ekkor a pont, A és A „hazugság egyik oldalán a PQ egyenes. ha k <0. то точки A и A' лежат по разные стороны от прямой PQ .

Megjegyzés: 1. Abban az esetben, ha | k | <1. рассматриваемое аффинное преобразование называют сжатием к прямой PQ. если же | k |> 1. hogy ez az átalakulás az úgynevezett tágulást.

Megjegyzés 2. Mi kell használni az adott tömörítés (feszültség) kijelölése

2. tömörítés (húzó) a két, előre meghatározott, egymásra merőleges irányban, amelyek előre meghatározott együtthatók kompressziós (expanziós)

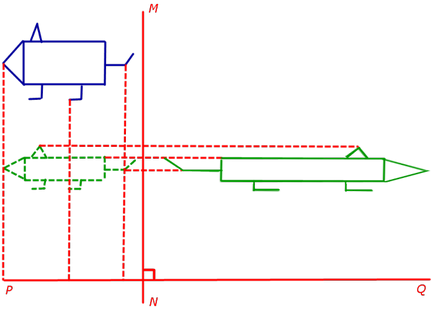
Legyen PQ és MN - két egymásra merőleges, egyenes vonalak, és a számok a K1 és K2 - tömörítési arányok (mellék) sík irányában vonalak PQ és MN, ill. Ezután a tömörítés (expanziós) mentén két egymásra merőleges irányban meghatározza a PQ és MN együtthatójú K1 és K2 (ábra10) nevezik kompressziót készítmény (nyújtatlan).

3. homotécia egy előre meghatározott homothetic központ és adja meg a tömörítési arány (expanziós)

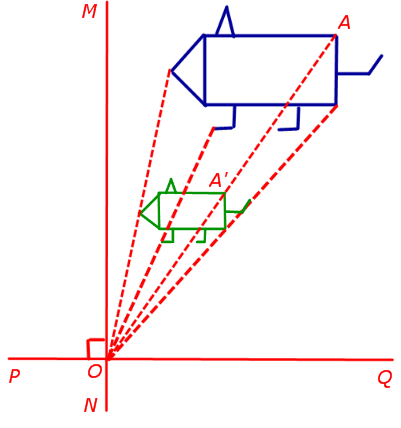
Homothety O középpontú és az együttható k nevezzük affin transzformáció, amelyben egy tetszőleges pontjában a síkban halad egy pont A „síkban, hogy a következő feltételek teljesülnek:

• pont „fekszik a vonalon AO;
• egyenlőség

ha k> 0. Ekkor a pont, A és A „hazugság egyik oldalán az a pont O., ha k <0. то точки A и A' лежат по разные стороны от точки O (рис.11).

Megjegyzés. Tekintsük két tetszőleges merőleges vonalak PQ és MN, metsző pontjában O. Ezután homothety a központ O és k együtthatót egybeesik a kompressziós (expanziós) a irányban PQ és MN együtthatójú k-val egyenlő. Más szóval, a tágítás a készítmény összehúzódások (rándulás):

4. átalakítása hasonlóság egy előre meghatározott skálázási tényező

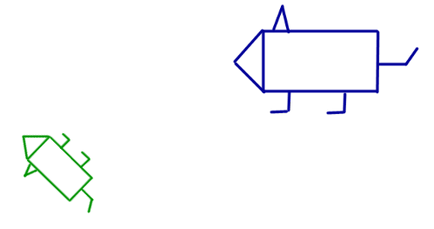
Hasonlósági transzformáció a hasonlósági koefficiens k úgynevezett affin transzformáció által képviselt összetételére nézve az a homothetic k együtthatót, és a mozgás (12.).

Osztályozása affin transzformációk a síkban

Azt is megismerkedhetnek a tanárok kifejlesztett egy képzési központ „rezolvens” tananyagok, hogy felkészüljenek a vizsgára és OGE (DPA) a matematikában.

A diákok, akik szeretnék jól felkészülni, és átmennek a vizsgán, vagy OGE (DPA) matematika, fizika vagy magyar nyelven a magas pontszámot, a képzési központ „rezolvens” tartja