Rendszeres számadatok és a test - studopediya

„Püthagorasz transzformált geometria, így ez a forma szabad tudomány, tekintve elveket pusztán elvont módon vizsgálja a tétel az immateriális javak és szellemi szempontból. Ő volt az, aki megtalálta az elmélet irracionális számok és szerkezete égitestek. " Így értékes hozzájárulást a Pitagorasz-geometria Proclus és ennek az összegnek ókori filozófus jogosan.

Tény, hogy az iskola Pitagorasz-geometria önálló tudományág. Ez volt Püthagorasz és követői voltak az elsők, rendszeresen tanulmányozza a geometria - mint elméleti tan tulajdonságainak absztrakt geometriai formák, nem pedig a receptek gyűjteménye által alkalmazott földmérő. Ebben az esetben a legfontosabb, a tulajdonságait geometriai alakzatok pithagoraszi nem határozott mérés közben egy logikai bizonyítás.

A legszélesebb területén a gyakorlati alkalmazás, a geometria a első tanításait a pitagoreusi # 956; # 940; # 952; # 951; # 956; # 945; Ledobta a fátylat a „titok”, és lett a legnépszerűbb a tudomány. Azonban a Iamblikhosz 'Life a Pitagorasz oka a népszerűség a geometria bemutatott némileg másképpen: „Így pitagoreusok miért geometria lett a nyilvánosság számára hozzáférhető. Ez volt a hiba az egyikük, amely elvesztette a pénzt Pitagorasz-közösségeket. Miután ez a katasztrófa közösség lehetővé tette számára, hogy pénzt keresni a geometria segítségével - a geometria az úgynevezett „Pitagorasz-hagyomány.” Szem előtt tartva, hogy a V. BC. e. Ezek nagyon népszerűek voltak a szofisták - vándor tanár a bölcsesség, ez elég lehet, hogy a pythagoreusok nem habozott, hogy töltse ki a kasszából a tanítás.

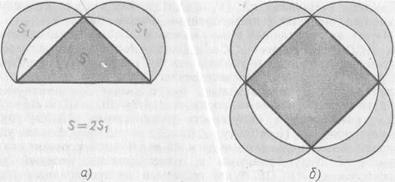
Így köszönhetően a Hippokratész, Chios, okunk van azt hinni, hogy a pythagoreusok általában úgy épülnek az egész síkrajzi egyenes vonalú formák. Vizsgálták a tulajdonságait háromszögek, négyszögek, paralelogramma trapéz bizonyult a tétel a szögek összege háromszögek, a tételt az oldalán a háromszög, amely felfekszik a tompaszög, az egyenlőség, a tétel a háromszögek. A csúcs a síkgeometria egyenes vonalú számok bizonyítéka volt a híres tétel Pitagorasz. Ezek az eredmények Pitagorasz-geometria, úgy tűnik, és én képezte az alapját a könyv „Elements” Euclid, azaz a Pitagorasz-tétel.

A pythagoreusok mutattak fokozott érdeklődést adatok helyes és szervek. A szabályos geometriai alakok miatt „helyes”, azaz a. E. jelenléte vagy forgatható tükör (és gyakran az egyik vagy a másik) a szimmetria, valamint lehetséges az egész pythagoreus reagál a rendszeres, szerkezetileg rendezett harmonikus a világegyetem felépítésébe. (Ez a kérdés vissza fogunk térni a sz. 2.2 és 4.3.) A geometriai forma, különösen a jobb, a legtöbb hatásosan mutatta a számot, és nem lehet több, alkalmas arra, hogy „kivonat számos dolgot.” Pitagorasz-lefektetett az egyik a másik geometriai formák (általában a jobb vagy a „hordozó” olyan „szent” szám), és hogy látták elérését koherencia jelenségek.

Éppen ezért a pythagoreusok különleges jelentőséget tulajdonítanak nekik bizonyította a tételt, miszerint egy síkban lehet teljesen (azaz nem „lyukak”, és átfedések ..), hogy az csak három szabályos sokszögek: háromszögek, négyzetek és hatszög (42. ábra). Ennek bizonyítéka tétel elég átlátható, és hagyjuk, hogy az olvasó számára. Ez nem nehéz, és az építőiparban a pontos számok és a számok azokból megduplázásával oldalon.

De most az építkezés egy szabályos ötszög már nem annyira nyilvánvaló. Nem tudjuk, hogyan kell megépíteni egy szabályos ötszög pythagoreusok. De azt is tudjuk, hogy az ötágú csillag - fő jelkép és azonosító jel - ezek alkotják a három egyenlő szárú háromszög. Ez egyértelműen visszhangozza építési módszerének egy szabályos ötszög, által leírt Euclid ( „Elements”, Vol. IV, dok. 11). Ahhoz, hogy a módszer Euclid, valószínűleg nyúlik vissza, a pythagoreusok. Tekintsük meg.

Mivel beírható kör egyenlő szárú háromszög ACD. aki. (A módszer építésének ilyen háromszög azt jelzi, c. 2.2.), És felhívni a felezővonal CE DB szögek C, illetve D. Ezután a sarkokban 1-5 (. 43. ábra) egyenlő, és ezért, egyenlő lesz a megfelelő ív és a szigorodó a húrt, azaz, ... Így írt a kör ABCDE egy szabályos ötszög. Mivel mind a szögek alapján azonos AB ív és az AE, illetve a szögek 1-7 egyenlő, és ennek következtében minden sarkában a ötszög ABCDE lesz, amely három, azonos szögben, azaz ... Így megkonstruált ötszög egyenlő oldalú és egyenlő szögű, t. E. Be.

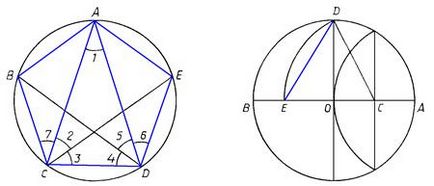
Idővel, a görög matematikus találtak egy könnyebb út építésére szabályos ötszög. Ezt a módszert az újabb kiemelkedő készítmény ókor - „Almagest” Ptolemaiosz (körülbelül 150), amely, mint a „kezdet” az euklideszi geometria, enciklopédia az ősi tudás a csillagászat. Ptolemaiosz osztja ketté kör sugara OA (C pont), és a CD kört ír le méretét, hogy az keresztezi AB átmérőjű pontban E (ábra. 44). Ezután ED az oldalán egy szabályos ötszög. (Miután elolvasta a bekezdés. 2.2 Az olvasó könnyen bizonyítani magad.)

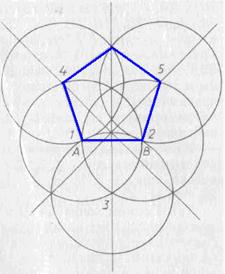
Újabb évezred és fél, 1525-ben Albreht Dyurer (1471-1528), egy festő és tudós, az egyik a titánok a Renaissance című értekezésében „Útmutató a mérési vonalzó segítségével és iránytű” hozzávetőleges eljárás létrehozunk egy szabályos ötszög egy adott oldalon AB a „rozsdás” iránytű, t. e. az egyik megoldás féknyereg. Módszer Dürer kitűnik a 45. ábra, ahol számok iránytű lábak következetesen azonosítottak. Dürer módszer különbözik nagy pontossággal (szögek 1 és 2 nem egyenlő 108 °, a. Angles 4. és 5. kissé nagyobb, mint 107 °, míg a C szög valamivel több, mint 109 °), úgy, hogy a hibák a szem nem teljesen érzékelhető. Dürer maga nem tett említést a közelítő jellegét az építés, esetleg tekintve, hogy pontos legyen. Mindazonáltal, a módszer a Durer hozzávetőleges. (Próbáld bizonyítani.)

És hogyan kell építeni segítségével egy vonalzót és iránytű követi a helyes összeg - heptagon? Ezt a feladatot ijesztő nemcsak az ősi pythagoreusoknál de megoldatlan maradt több mint két évezreddel! Csak 1796-ban, 19 éves német fiú Carl Friedrich Gauss (1777-1855), becenevén a király később matematikusok megoldotta. Gauss azt mutatja, hogy a problémát építésének egy vonalzó és iránytű korrekt N-gon, egyenértékű a probléma a elosztjuk a kört n egyenlő részre, ez együtt jár a gyökerei a tanulmány. Továbbá Gauss bebizonyította, hogy a szabályos n-szög lehet kialakítani az uralkodó és iránytű akkor és csak akkor, ha az N - elsődleges formájának

Prime számok formájában (2.1.1), amelyekre a gazdaságok száma, és mégis csak öt ilyen szám :.

Ez a Gauss eredmény általánosítható az esetben, amikor a száma a sokszög oldalainak n a termék a számok a forma (2.1.1). Figyelembe véve még a lehetőségét duplájára n. Megfogalmazzuk a Gauss-tétel. szabályos sokszög lehet előállítani iránytű és vonalzó akkor és csak akkor, ha a szám az oldalán a formája

Valójában. mivel más Fermat szám ez még nem ismert.

Könnyen belátható, hogy a poligonok tudtak építeni az ókori görögök, vagyis azok, akik. szereplő (2.1.2). Így, hozzátéve, az új antik poligonok n = 17, 34, 51, 68, 85, 126, 252, 255, és 257. Az új elv ezek közül 17-gon-gon 257 és 65 537 gon. Gauss talált egy módszert építésének első két sokszög. Megjegyezzük, hogy a módszer leírását építése 257-gon Gauss vett mintegy ötven oldal. Gauss élettartama rendkívül büszke ifjúkori felfedezése és hagyott vésett a sírkövére szabályos 17-szög írt egy kört.

Így egy szabályos sokszög konstrukció vonalzót és iránytű lehetséges, ha n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, .... nem, ha n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33.

Most rátérünk a rendszeres poliéder. Már csak öt, és Proclus mellett figyelemre méltó felfedezések síkgeometria tulajdonítja Püthagorasz az építőiparban az öt szabályos szilárd. Ma azonban a matematikusok, történészek inkább azt hinni, nem átkozott, és úgy találta, scholium (# 963; # 967; # 972; # 955; # 953; # 959; # 957; - értelmezés, magyarázat) a XIII könyv "Elements" Euclid, ahol azt mondja, Püthagorasz tudta csak három helyes test - a tetraéder, kocka (kocka) és dodekaéder, majd kinyitotta a Theaitétosz és a maradék kettő - az oktaéder és ikozaéder. Ebben és a másik esetben, az ősi bizonyíték meséljen az érdeklődés a pythagoreusok a megfelelő szervek.

Úgy tűnik, hogy a természet maga is ösztönözte a pythagoreusok formájában rendszeres telefonos: só kristályok alakja egy kocka, alum - oktaéder, és a kristályok pirit - dodekaéder. Végül, ahogy azt az ásatások Olaszországban, ez volt a kedvenc játék etvengerskih gyerekek az idő Püthagorasz.

A név egy szabályos poliéder van megadva száma éle (például egy tetraéder - # 964; # 949; # 964; # 961; # 940 - # 949; # 948; # 961; # 959; # 957; - # 964; # 949; # 964; # 961; # 940; # 962; - chetype + # 949; # 963; # 961; # 945; - egy olyan terület a test, az arc - tetraéder). Rendszeres polihedront a 46. ábrán látható, és azok geometriai jellemzői táblázatban foglaljuk össze, ahol m jelentése az arcok a vertex.

A pythagoreusok észrevette, hogy a kocka a csúcsok száma (8) van a harmonikus átlagát arcok száma (6) és a bordák száma (12), és ezért nevezik a köbös szervezet harmonikus. kocka különleges küldetése volt látható is az a tény, hogy ő volt az egyetlen szabályos szilárd teljesen kitölti a teret.

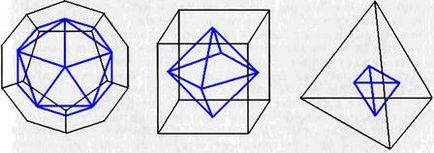
Abban az időben a Euclid, megjegyezték, hogy a kocka és az oktaéder, dodekaéder és ikozaéder kettős (dual), t. E. A arcok számát a test megegyezik a csúcsok száma a másik, és fordítva. Ezután, egy test lehet beszerezni a másik, ha a centroid a arcok, hogy elfogadja csúcsai a másik, vagy fordítva (ábra. 46). Tetraéder kettős önmagához.

Azonban a legfontosabb tulajdonsága konvex poliéderek találtuk csak a közepén a XVIII. Euler-tétel. bármely számú csúcsai egy konvex poliéder (L), plusz az arcok száma (M) mínusz a száma ig (N) egy egyenlő állandó érték két:

És mégis a legérdekesebb jellemzője szabályos szilárd, hogy léteznek csak öt. Nem véletlen az igazolás ezt a tényt befejeződött utolsó XIII könyv „Elements” Euclid. [44] Tény, hogy a mennyisége S sík a vertex szögek a konvex poliéder kell szigorúan kisebb, mint 360 °, míg az arcok száma a csúcs. Így néz szabályos szilárd lehet csak három szabályos sokszögek: háromszög, négyszög, ötszög, hatszög, mert még. akkor lehet, hogy három helyes test egyenlő oldalú háromszög: - a tetraéder - oktaéder és a - ikozaéder (a). Terek és rendszeres ötszög - csak egy (kocka dodekaéder), amikor (ha - a terek és - ötszög). Így a rendszeres poliéderek is csak öt.

Ez a tény nem maradhat közömbös hajlamos numerikus misztika pythagoreusoknál és mögöttük, Platón és a újplatonikusok. Plato kifejlesztett a híres tanát az öt „elemek” - alapján a világegyetem, az atomok, amelyek úgy dolgozták formájában szabályos szilárd. (Több Plato ez a tan tárgyaljuk para. 4.3.) Azóta, szabályos testek gyakran nevezik platóni testek.

Rendszeres poliéder egész emberiség történetében nem szűnik meg csodálni a szimmetria érdeklődő elme, a bölcsesség és a tökéletesség formáját. Leonardo da Vinci szereti bütyköl csontvázak szabályos szilárd, és azokat, mint egy ajándék az arisztokrácia, esetleg egy kísérletet, hogy rögzítse a hatalom a filozófiai reflexió a szépség, az örök igazságok (ábra. 47).

Ábra. 47. Rajzok fa modell a dodekaéder és ikozaéder által készített Leonardo da Vinci egy könyvet barátja Luca Pacioli „A Isteni.” Velencében. 1509

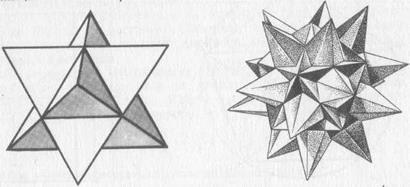
Ábra. 48. ábra. 49. A hetedik csillag alakú Archimedes body - ikozidodekaéder.